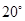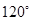题目内容
如图,OM⊥ON.已知边长为2的正三角形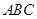
，两顶点
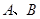分别射线OM,ON上滑动，当∠OAB = 21°时, ∠NBC = 。滑动过程中，连结OC，则OC的长的最大值是 。
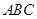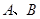，两顶点分别射线OM,ON上滑动，当∠OAB = 21°时, ∠NBC = 。滑动过程中，连结OC，则OC的长的最大值是 。51O ， 
.
.试题分析：等边三角形各内角为60°，
∵∠NBC=180°-∠ABC-∠ABO，∠ABO=90°-∠OAB，∠OAB=21°，
∴∠NBC=51°；
取AB中点D，连OD，DC，有OC≤OD+DC，
当O、D、C共线时，OC有最大值，最大值是OD+CD．
∵△ABC为等边三角形，D为中点，
∴BD=1，BC=2，根据勾股定理得：CD=
，又△AOB为直角三角形，D为斜边AB的中点，
∴OD=
AB=1，∴OD+CD=1+
，即OC的最大值为1+．故答案为：51°；1+
点评：找出OC最大时的长为CD+OD是解本题的关键．
练习册系列答案
相关题目
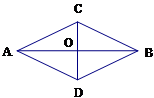
，M、N分别是AC、BD的中点，猜一猜MN与BD的位置关系，并说明结论。
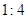，则这个等腰三角形顶角的度数为（ ）
