题目内容
【题目】如图,一位篮球运动员在距离篮圈中心水平距离![]() 处跳起投篮,球沿一条抛物线运动,当球运动的水平距离为
处跳起投篮,球沿一条抛物线运动,当球运动的水平距离为![]() 时,达到最大高度
时,达到最大高度![]() ,然后准确落入篮筐内,已知篮圈中心距离地面高度为
,然后准确落入篮筐内,已知篮圈中心距离地面高度为![]() ,试解答下列问题:
,试解答下列问题:
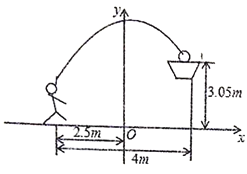
(1)建立图中所示的平面直角坐标系,求抛物线所对应的函数表达式.
(2)这次跳投时,球出手处离地面多高?
【答案】(1)![]() ;(2)这次跳投时,球出手处离地面
;(2)这次跳投时,球出手处离地面![]() .
.
【解析】
(1)设抛物线的表达式为y=ax2+3.5,依题意可知图象经过的坐标,由此可得a的值;
(2)设这次跳投时,球出手处离地面hm,因为(1)中求得y=-0.2x2+3.5,当x=-2,5时,即可求得结论.
解:(1)∵抛物线的顶点坐标为![]() ,
,
∴可设抛物线的函数关系式为![]() .
.
∵篮圈中心![]() 在抛物线上,将它的坐标代入上式,得
在抛物线上,将它的坐标代入上式,得![]() ,
,
∴![]() ,
,
∴![]()
(2)设这次跳投时,球出手处离地面![]() ,
,
因为(1)中求得![]() ,
,
∴当![]() 时,
时,
![]() .
.
∴这次跳投时,球出手处离地面![]() .
.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目