题目内容
【题目】如图，在由边长都为1的小正方形组成的网格中，点B，M均为格点，点A为小正方形边的中点．
（I）线段
的长为____________；
（Ⅱ）在线段上存在一点N，使得点N满足
，请你借助给定的网格，用无刻度的直尺作出
，并简要说明你是怎么找到点N的．（不要求证明）_________________________________________．
【答案】（I）
；（Ⅱ）取格点E、F、G、H，连接
、
得到点C；连接
，交线段
于点N；则点N即为所求；图见解析．
【解析】
（I）利用勾股定理求出AB的长即可；
（II）构造等腰直角三角形MDC，使直角边长等于AB，而且其中MD⊥AB，CD//AB，连接，交线段于点N；则点N即为所求；
（Ⅰ）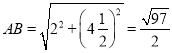
，
故答案为：；
（Ⅱ）如图，取格点E、F、G、H，连接、得到点C；连接，交线段于点N；则点N即为所求．
理由：先作正方形对角线的交点C，连接交于点N，再确定正方形边上的中点D，则
，
，连接
，则
为等腰直角三角形，所以
，所以
．
练习册系列答案
相关题目
【题目】某学校计划组织1200名师生参加社会实践活动，其中包括25名教师与某公交公司洽谈后得知该公司有A、B型两种客车．每辆A型客车载客54人，租金480元；每辆B型客车载客36人，租金280元．由于每辆车上要求有一名教师，决定租用25辆客车．
设租用A型客车x辆（x为非负整数）．
（Ⅰ）根据题意填写下表：
客车类型 | 车辆数（辆） | 载客数（人） | 租金（元） |
A型客车 | x | ||
B型客车 |
|
（Ⅱ）若租车总费用为10800元，怎样安排车辆？
（Ⅲ）采取怎样的租车方案可以使租车总费用最低，最低是多少元？
