题目内容
【题目】给定直线l:y=kx,抛物线C:y=ax2+bx+1.
(1)当b=1时,l与C相交于A,B两点,其中A为C的顶点,B与A关于原点对称,求a的值;
(2)若把直线l向上平移k2+1个单位长度得到直线l′,则无论非零实数k取何值,直线l′与抛物线C都只有一个交点.
①求此抛物线的解析式;
②若P是此抛物线上任一点,过P作PQ∥y轴且与直线y=2交于Q点,O为原点.求证:OP=PQ.
【答案】
(1)
∵l:y=kx,C:y=ax2+bx+1,当b=1时有A,B两交点,
∴A,B两点的横坐标满足kx=ax2+x+1,即ax2+(1﹣k)x+1=0.
∵B与A关于原点对称,
∴0=xA+xB= ![]() ,
,
∴k=1.
∵y=ax2+x+1=a(x+ ![]() )2+1﹣
)2+1﹣ ![]() ,
,
∴顶点(﹣ ![]() ,1﹣
,1﹣ ![]() )在y=x上,
)在y=x上,
∴﹣ ![]() =1﹣
=1﹣ ![]() ,
,
解得 a=﹣ ![]() .
.
(2)
①解:∵无论非零实数k取何值,直线l′与抛物线C都只有一个交点,
∴k=1时,k=2时,直线l′与抛物线C都只有一个交点.
当k=1时,l′:y=x+2,
∴代入C:y=ax2+bx+1中,有ax2+(b﹣1)x﹣1=0,
∵△=(b﹣1)2+4a=0,
∴(b﹣1)2+4a=0,
当k=2时,l′:y=2x+5,
∴代入C:y=ax2+bx+1中,有ax2+(b﹣2)x﹣4=0,
∵△=(b﹣2)2+16a=0,
∴(b﹣2)2+16a=0,
∴联立得关于a,b的方程组 ![]() ,
,
解得 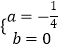 或
或 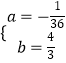 .
.
∵l′:y=kx+k2+1代入C:y=ax2+bx+1,得ax2+(b﹣k)x﹣k2=0,
∴△=(b﹣k)2+4ak2.
当 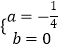 时,△=(﹣k)2+4×(﹣
时,△=(﹣k)2+4×(﹣ ![]() )k2=k2﹣k2=0,故无论k取何值,直线l′与抛物线C都只有一个交点.
)k2=k2﹣k2=0,故无论k取何值,直线l′与抛物线C都只有一个交点.
当 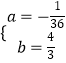 时,△=(
时,△=( ![]() ﹣k)2+4×(﹣
﹣k)2+4×(﹣ ![]() )k2=
)k2= ![]() k2﹣
k2﹣ ![]() k+
k+ ![]() ,显然虽k值的变化,△不恒为0,所以不合题意舍去.
,显然虽k值的变化,△不恒为0,所以不合题意舍去.
∴C:y=﹣ ![]() x2+1.
x2+1.
②证明:根据题意,画出图象如图1,
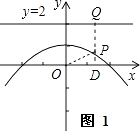
由P在抛物线y=﹣ ![]() x2+1上,设P坐标为(x,﹣
x2+1上,设P坐标为(x,﹣ ![]() x2+1),连接OP,过P作PQ⊥直线y=2于Q,作PD⊥x轴于D,
x2+1),连接OP,过P作PQ⊥直线y=2于Q,作PD⊥x轴于D,
∵PD=|﹣ ![]() x2+1|,OD=|x|,
x2+1|,OD=|x|,
∴OP= ![]() =
= ![]() =
= ![]() =
= ![]() x2+1,
x2+1,
PQ=2﹣yP=2﹣(﹣ ![]() x2+1)=
x2+1)= ![]() x2+1,
x2+1,
∴OP=PQ.
【解析】(1)直线与抛物线的交点B与A关于原点对称,即横纵坐标对应互为相反数,即相加为零,这很适用于韦达定理.由其中有涉及顶点,考虑顶点式易得a值.(2)①直线l:y=kx向上平移k2+1,得直线l′:y=kx+k2+1.根据无论非零实数k取何值,直线l′与抛物线C:y=ax2+bx+1都只有一个交点,得ax2+(b﹣k)x﹣k2=0中△=(b﹣k)2+4ak2=0.这虽然是个方程,但无法求解.这里可以考虑一个数学技巧,既然k取任何值都成立,那么代入最简单的1,2肯定是成立的,所以可以代入试验,进而可求得关于a,b的方程组,则a,b可能的值易得.但要注意答案中,可能有的只能满足k=1,2时,并不满足任意实数k,所以可以再代回△=(b﹣k)2+4ak2中,若不能使其结果为0,则应舍去.
②求证OP=PQ,那么首先应画出大致的示意图.发现图中几何条件较少,所以考虑用坐标转化求出OP,PQ的值,再进行比较.这里也有数学技巧,讨论动点P在抛物线y=﹣ ![]() x2+1上,则可设其坐标为(x,﹣
x2+1上,则可设其坐标为(x,﹣ ![]() x2+1),进而易求OP,PQ.
x2+1),进而易求OP,PQ.
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识,掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.

【题目】现今“微信运动”被越来越多的人关注和喜爱,某兴趣小组随机调查了我市50名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
步数 | 频数 | 频率 |
0≤x<4000 | 8 | a |
4000≤x<8000 | 15 | 0.3 |
8000≤x<12000 | 12 | b |
12000≤x<16000 | c | 0.2 |
16000≤x<20000 | 3 | 0.06 |
20000≤x<24000 | d | 0.04 |
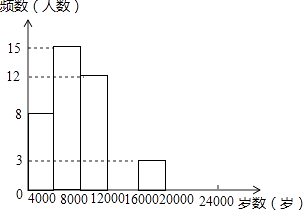
请根据以上信息,解答下列问题:
(1)写出a,b,c,d的值并补全频数分布直方图;
(2)本市约有37800名教师,用调查的样本数据估计日行走步数超过12000步(包含12000步)的教师有多少名?
(3)若在50名被调查的教师中,选取日行走步数超过16000步(包含16000步的两名教师与大家分享心得,求被选取的两名教师恰好都在20000步(包含20000步)以上的概率.





