题目内容
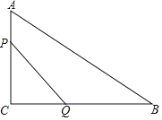
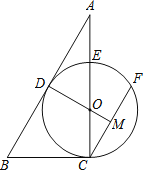
【题目】如图,在△ABC中,点O在边AC上,⊙O与△ABC的边BC,AB分别相切于C,D两点,与边AC交于E点,弦CF与AB平行,与DO的延长线交于M点.
(1)求证:点M是CF的中点;
(2)若E是![]() 的中点,BC=a,
的中点,BC=a,
①求![]() 的弧长;
的弧长;
②求![]() 的值.
的值.
【答案】(1)见解析;(2)①![]() πa;②
πa;②![]() =1.
=1.
【解析】
(1)由切线的性质可得∠ACB=∠ODB=90°,由平行线的性质可得OM⊥CF,由垂径定理可得结论;
(2)①由题意可证△BCD是等边三角形,可得∠B=60°,由直角三角形的性质可得AB=2a,AC=![]() a,AD=a,通过证明△ADO∽△ACB,可得
a,AD=a,通过证明△ADO∽△ACB,可得![]() ,可求DO的长,由弧长公式可求解;
,可求DO的长,由弧长公式可求解;
②由直角三角形的性质可求AO=![]() a,可得AE的长,即可求解.
a,可得AE的长,即可求解.
证明:(1)∵⊙O与△ABC的边BC,AB分别相切于C,D两点,
∴∠ACB=∠ODB=90°,
∵CF∥AB,
∴∠OMF=∠ODB=90°,
∴OM⊥CF,且OM过圆心O,
∴点M是CF的中点;
(2)①连接CD,DF,OF,
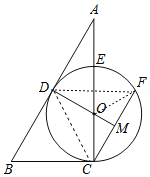
∵⊙O与△ABC的边BC,AB分别相切于C,D两点,
∴BD=BC,
∵E是![]() 的中点,
的中点,
∴![]() ,
,
∴∠DCE=∠FCE,
∵AB∥CF,
∴∠A=∠ECF=∠ACD,
∴AD=CD,
∵∠A+∠B=90°,∠ACD+∠BCD=90°,
∴∠B=∠BCD,
∴BD=CD,且BD=BC,
∴BD=BC=CD,
∴△BCD是等边三角形,
∴∠B=60°,
∴∠A=30°=∠ECF=∠ACD,
∴∠DCF=60°,
∴∠DOF=120°,
∵BC=a,∠A=30°,
∴AB=2a,AC=![]() a,
a,
∴AD=a,
∵∠A=∠A,∠ADO=∠ACB=90°,
∴△ADO∽△ACB,
∴![]() ,
,
∴![]()
∴DO=![]() a,
a,
∴![]() 的弧长=
的弧长=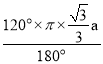 =
=![]() πa;
πa;
②∵∠A=30°,OD⊥AB,
∴AO=2DO=![]() a,
a,
∴AE=AO﹣OE=![]() ﹣
﹣![]() a=
a=![]() a,
a,
∴![]() =1.
=1.