��Ŀ����
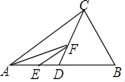
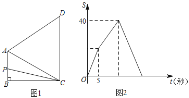
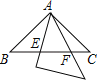
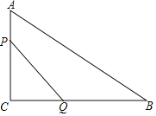
����Ŀ����ͼ��Rt��ABC�У���ACB��90�㣬AC��6cm��BC��8cm����P�ӵ�A��������ÿ��1cm���ٶ���AC�˶���ͬʱ��Q�ӵ�C��������ÿ��2cm���ٶ���CB�˶�����Q�����Bʱ����Pͬʱֹͣ�˶���
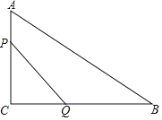
��1�����˶�����ʱ��PCQ�����Ϊ5cm2��
��2����PCQ������ܷ����10cm2�����ܣ�����˶�ʱ�䣬�����ܣ�˵�����ɣ�
��3���Ƿ����ij��ʱ��t��ʹ�ı���ABQP�������С�������ڣ�����˶�ʱ�䣬�����ܣ�˵�����ɣ�
���𰸡���1������1���PCQ���������5cm2����2�����ܣ�����������3��![]() ʱ��ʹ�ı���ABQP�������С
ʱ��ʹ�ı���ABQP�������С
��������
��1�����˶�t����PCQ���������5cm2���ֱ��ʾ���߶�CP���߶�CQ�ij��������������ε������ʽ�г�������⼴�ɣ�
��2�����������ε������ʽ�г����̣��õ��ķ�����ʵ���⣬˵����PCQ��������ܵ���10cm2��
��3����ʾ���ı���ABQP�������Ȼ�������䷽���������Сֵ���ɣ�
��1�����˶�t����PCQ���������5cm��
��������ã�
CP=6��t��QC=2t��
���PCQ������ǣ�![]() CQCP=
CQCP=![]() ��(6��t)��2t=5��
��(6��t)��2t=5��
��ã�t1=1��t2=5����ȥ����
�ʾ���1���PCQ���������5cm2��
��2������PCQ������ܷ����10cm2����![]() ��(6��t)��2t=10��
��(6��t)��2t=10��
����ã�![]() ��
��
![]() ��
��
���Է�����ʵ���⣬��PCQ��������ܵ���10cm2��
��3��![]() =
=![]()
![]() ��
��
��Ϊ![]() >0��
>0��
�����ı���ABQP���������Сֵ��
��![]() ��
��
��![]() ʱ���ı���ABQP���������СֵΪ
ʱ���ı���ABQP���������СֵΪ![]() ��
��

 ��У����ϵ�д�
��У����ϵ�д�