题目内容
【题目】我们定义：有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.
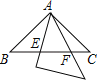
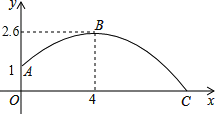
（1）已知：如图，四边形ABCD是“等对角四边形”， 
,则∠C= ;
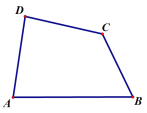
（2）已知：在“等对角四边形”ABCD中，∠DAB=60°，∠ABC=90°，AB=4 , AD=3.求对角线AC的长；
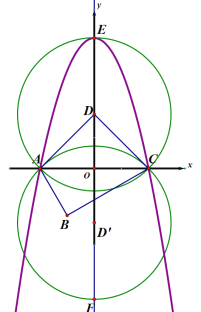
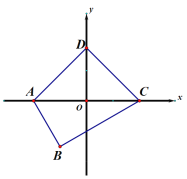
（3）已知：如图，在平面直角坐标系xoy中，四边形ABCD是“等对角四边形”，其中
,点D在y轴上，抛物线
过点A、C,点P在抛物线上，当满足
的P点至少有3个时,总有不等式
成立，求n 的取值范围.
【答案】（1）115°；（2）
或
；（3）
【解析】
（1）根据“等对角四边形”的概念即可求解；
（2）分两种情况：①当∠B=∠D=90°时延长AD,BC交于点E，先用含30°角的直角三角形的性质求出BE， DE，再用三角函数求出CE，即可得到BC，由勾股定理求出AC；②当∠A=∠C=60°时,过D分别作DE⊥AB于E,DF⊥BC于点F，先用含30°角的直角三角形的性质求出DE，CF，得到BC，由勾股定理求出AC；
（3）根据题意求出D（0,2），设抛物线解析式为
，
，以D（0,2）为圆心，AD长为半径作⊙D，以D’（0，-2）为圆心，AD长为半径作⊙D’，如图所示,⊙D交y轴正半轴于点E,⊙D’交y轴负半轴于点F.当点P在优弧AEC和优弧AFC上时
，当抛物线过E点时满足题意的P点有3个，
，当满足的P点至少有3个时
，依次求解即可.
解：（1）由题意可得：∠B=∠D=85°，则∠C=360°-85°×2-75°=115°；
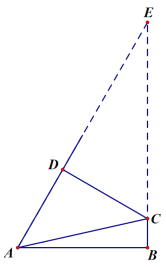
（2）①如图，∠B=∠D=90°时延长AD,BC交于点E
∵∠DAB=60°
∴∠E=30°
又 ∵AB=4,AD=3
∴
∴
∴
∴
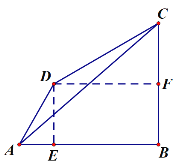
②如图，∠A=∠C=60°时,过D分别作DE⊥AB于E,DF⊥BC于点F
∵∠DAB=∠BCD=60°
又 ∵AB=4,AD=3
∴
∴
∴
∴
综上，
（3）∵
∴
∴
∴∠ABC=90°
∵
,
∴
∵四边形ABCD是“等对角四边形”
∴
∴D（0,2）
∵抛物线
过点A、C,
∴
∴
，
以D（0,2）为圆心，AD长为半径作⊙D，以D’（0，-2）为圆心，AD长为半径作⊙D’，如图所示,⊙D交y轴正半轴于点E,⊙D’交y轴负半轴于点F.当点P在优弧AEC和优弧AFC上时，当抛物线过E点时满足题意的P点有3个，
此时，
当满足的P点至少有3个时，
当时，
∵总有不等式
成立
∴
∴
