题目内容
如图，O是△ABC的内心，过点O作EF∥AB，与AC、BC分别交E、F，则( )
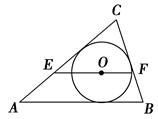
A．EF＞AE＋BF
B．EF＜AE＋BF
C．EF＝AE＋BF
D．EF≤AE＋BF
A．EF＞AE＋BF
B．EF＜AE＋BF
C．EF＝AE＋BF
D．EF≤AE＋BF
C
连接OA、OB，
∵O是△ABC的内心，
∴OA、OB分别是∠CAB及∠ABC的平分线，
∴∠EAO＝∠OAB，∠ABO＝∠FBO，∵EF∥AB，
∴∠AOE＝∠OAB，
∠BOF＝∠ABO，
∴∠EAO＝∠AOE，
∠FBO＝∠BOF，
∴AE＝OE，OF＝BF，
∴EF＝AE＋BF，
故选C.
∵O是△ABC的内心，
∴OA、OB分别是∠CAB及∠ABC的平分线，
∴∠EAO＝∠OAB，∠ABO＝∠FBO，∵EF∥AB，
∴∠AOE＝∠OAB，
∠BOF＝∠ABO，
∴∠EAO＝∠AOE，
∠FBO＝∠BOF，
∴AE＝OE，OF＝BF，
∴EF＝AE＋BF，
故选C.
练习册系列答案
阅读快车系列答案
相关题目
是恒成立的．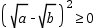
恒成立，说明
