题目内容
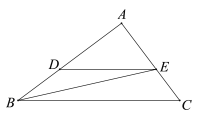
【题目】如图，在Rt△ABC中，∠A=90°．AB=8cm，AC=6cm，若动点D从B出发，沿线段BA运动到点A为止（不考虑D与B，A重合的情况），运动速度为2cm/s，过点D作DE∥BC交AC于点E，连接BE，设动点D运动的时间为x（s），AE的长为y（cm）．
（1）求y关于x的函数表达式，并写出自变量x的取值范围；
（2）当x为何值时，△BDE的面积S有最大值？最大值为多少？
【答案】（1）
(0＜x＜4)；（2）当x=2时，S△BDE最大，最大值为6cm2．
【解析】
（1）根据已知条件DE∥BC可以判定△ADE∽△ABC；然后利用相似三角形的对应边成比例求得
；最后用x、y表示该比例式中的线段的长度；
（2）根据∠A=90°得出S△BDE=
BDAE，从而得到一个面积与x的二次函数，从而求出最大值；
（1）动点D运动x秒后，BD=2x．
又∵AB=8，∴AD=8-2x．
∵DE∥BC，∴，∴
，
∴y关于x的函数关系式为
(0＜x＜4)．
（2）解：S△BDE=
=
(0＜x＜4)．
当
时，S△BDE最大，最大值为6cm2．
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
