题目内容
【题目】甲、乙、丙,丁四个人做“击鼓传花”游戏,游戏规则是:第一次由甲将花随机传给乙、丙、丁三人中的某一人中的某一人,以后的每一次传花都是由接到花的人随机传给其他三人中的某一人.
(1)甲第一次传花时,恰好传给乙的概率是 ;
(2)求经过两次传花,花恰好回到甲手中的概率;
(3)经过三次传花,花落在丙手上的概率记作P1,落在丁手上的概率记作P2,则P1 P2(填“>”、“<”或者“=”)
【答案】(1)![]() ;(2)P(第2次传球后球回到甲手里)=
;(2)P(第2次传球后球回到甲手里)=![]() ;(3)=.
;(3)=.
【解析】
(1)直接利用概率公式计算可得;
(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两次传球后,球恰在甲手中的情况,再利用概率公式即可求得答案;
(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与三次传球后,球恰在丙、丁手中的情况,再利用概率公式即可求得答案.
(1)甲第一次传花时,恰好传给乙的概率是![]() ,
,
故答案为:![]() ;
;
(2)画树状图:
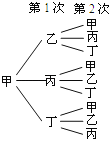
共有9种等可能的结果,其中符合要求的结果有3种,
∴P(第2次传球后球回到甲手里)=![]() =
=![]() .
.
(3)画树状图如下,

由树状图知经过三次传花共有27种等可能结果,其中花落在丙手上的有7种结果,花落在丁手上的有7种结果,
∴P1=![]() 、P2=
、P2=![]() ,
,
则P1=P2,
故答案为:=.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目