Question

已知抛物线的顶点为（0，4）且与x轴交于（-2，0），（2，0）．

（1）直接写出抛物线解析式；
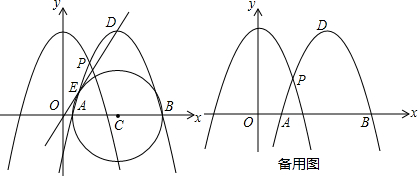
（2）如图，将抛物线向右平移k个单位，设平移后抛物线的顶点为D，与x轴的交点为A、B，与原抛物线的交点为P．
①当直线OD与以AB为直径的圆相切于E时，求此时k的值；
②是否存在这样的k值，使得点O、P、D三点恰好在同一条直线上？若存在，求出k值；若不存在，请说明理由．

Answer 1

（1）∵抛物线的顶点为（0，4），
∴可设抛物线解析式为y=ax²+4，
又∵抛物线过点（2，0），
∴0=4a+4，解得a=-1，
∴抛物线解析式为y=-x²+4；

（2）①如图，连接CE，CD．
∵OD是⊙C的切线，∴CE⊥OD．
在Rt△CDE中，∠CED=90°，CE=AC=2，DC=4，
∴∠EDC=30°，
∴在Rt△CDO中，∠OCD=90°，CD=4，∠ODC=30°，
∴OC=

4 3

3

，
∴当直线OD与以AB为直径的圆相切时，k=OC=

4 3

3

；

②存在k=2

2

，能够使得点O、P、D三点恰好在同一条直线上．理由如下：
设抛物线y=-x²+4向右平移k个单位后的解析式是y=-（x-k）²+4，它与y=-x²+4交于点P，
由-（x-k）²+4=-x²+4，解得x₁=

k

2

，x₂=0（不合题意舍去），
当x=

k

2

时，y=-

1

4

k²+4，
∴点P的坐标是（

k

2

，-

1

4

k²+4）．
设直线OD的解析式为y=mx，把D（k，4）代入，
得mk=4，解得m=

4

k

，
∴直线OD的解析式为y=

4

k

x，
若点P（

k

2

，-

1

4

k²+4）在直线y=

4

k

x上，得-

1

4

k²+4=

4

k

•

k

2

，
解得k=±2

2

（负值舍去），
∴当k=2

2

时，O、P、D三点在同一条直线上．