Question

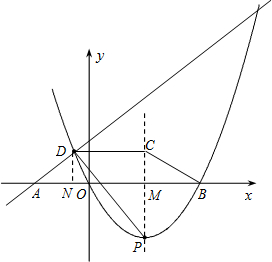
如图，四边形ABCD是梯形，sin∠OAD=tan∠OBC=

2

3

，PC是抛物线的对称轴，且P（3，-3）．
（1）求抛物线的函数表达式；
（2）求点D的坐标；
（3）求直线AD的函数表达式；
（4）PD与AD垂直吗？

Answer 1

（1）根据图象可得出抛物线经过点O（0，0）和顶点坐标为P（3，-3），
故可得出解析式为：y=a（x-3） ²-3，
将（0，0）代入得出：a=

1

3

，
故抛物线解析式为：y=

1

3

（x-3） ²-3=

1

3

x²-2x；

（2）∵PC是抛物线的对称轴，且P（3，-3），
∴BM=3，
∵tan∠OBC=

CM

BM

=

2

3

，
∴CM=2，
∴点D的纵坐标为2．
2=

1

3

x2-2x，
解得x₁=3+

15

（不合题意舍去），x₂=3-

15

，
∴D(3-

15

，2)．

（3）过点D作DN⊥x轴于点N，
∵DN=2，sin∠OAD=

DN

AD

=

2

3

，
∴AD=3，
∴AN=

5

．
∴A点坐标为：（3-

5

-

15

，0），
把A，D的坐标代入y=kx+b，得：

(3- 5 - 15 )k+b=0 (3- 15 )k+b=2

，
解得：

k= 2 5 5 b=2+2 3 - 6 5 5

，
即y=

2 5

5

x+2+2

3

-

6 5

5

；

（4）∵CD=NO+OM=

15

-3+3=

15

，CP=CM+PM=3+2=5，
∵tan∠DPC=

CD

PC

=

15

5

，
tan∠DAN=

DN

AN

=

2

5

，
∴

15

5

≠

2

5

，
∴∠CPD≠∠DAN，
∵∠CPD=NDP，
∴∠PDN≠∠DAN，
∵∠DAN+∠ADN=90°，
∴∠ADN+∠NDP≠90°，
∴PD与AD不垂直．