题目内容
【题目】如图,已知![]() ,
,![]() ,
,![]() ,则
,则![]() ( )
( )
A. ![]() B. 16C.
B. 16C. ![]() D.
D. ![]()
【答案】C
【解析】
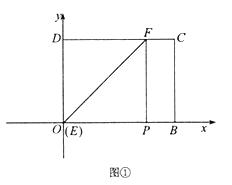
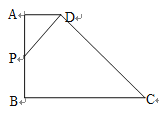
作DE⊥BC于E,则∠DEC=90°,四边形ABED是矩形,得出DE=AB=AP+PB=8,BE=AD=3,证出∠CDE=∠PDA,得出△CDE∽△PDA,得出对应边成比例![]() =
=![]() ,求出CE,即可得出BC的长.
,求出CE,即可得出BC的长.
解:作DE⊥BC于E,如图所示:
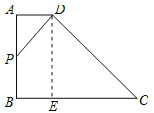
则DEC=90°,四边形ABED是矩形,
∴DE=AB=AP+PB=8,BE=AD=3,∠ADE=90°,
∵∠CDP=90°,
SY5∠CDE=∠PDA,
又∵∠DPA=90°=∠DEC,
∴△CDE∽△PDA,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴CE=![]() ,
,
∴BC=BE+CE=3+![]() =
=![]() ;
;
故选C.
“点睛”本题考查了相似三角形的判定与性质,矩形的判定与性质;熟练掌握矩形的判定与性质,证明三角形相似得出比例式是解决问题的关键.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目