��Ŀ����
����Ŀ������֪�������������Ĺ��̳�Ϊ֤����֤���ij�����������ǻ�����ʵ.֤��������ȫ�ȵĻ�����ʵ�У�������нǷֱ���ȵ�����������ȫ�ȣ����Ǽ���б߷ֱ���ȵ�����������ȫ�ȣ����߷ֱ���ȵ�����������ȫ��.
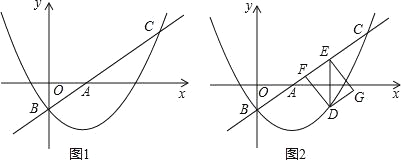
��1����ѡ���������ϻ�����ʵ���������ڽǺͶ������������ͼ�Σ�֤�������Ƿֱ����������һ��ȽǵĶԱ���ȵ�����������ȫ��.

��2���������ε������ߺ�������ͳ��Ϊ�����ε�����Ԫ��.����������������ĶԶ�ӦԪ����ȣ�������������һ��ȫ������˵������.
���𰸡���1��֤������⣻��2������������һ��ȫ�ȣ����ɼ����.
��������
��1��ͨ��������Ⱥ��������ڽǺͶ�����֪��������Ҳ��ȣ�Ȼ���������Ǽ��б߷ֱ���ȼ���֤����������ȫ�ȣ�
��2���ĶԶ�ӦԪ����ȣ��ɷ��������: ���������ߺ���һ�Ƕ�Ӧ��ȣ����������ߺ������Ƕ�Ӧ��ȣ� ���������Ǻ���һ�߶�Ӧ��ȣ�������������ۼ���.
��1����֪��![]() ֤����
֤����![]()
֤������![]() ��
��![]()
�֡�![]()
��![]()
��![]() ��
��![]() ��
�У�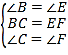
��![]()
��2������������һ��ȫ�ȣ��������£�
������������ߺ���һ�Ƕ�Ӧ��ȣ�����SSS֤����������ȫ�ȣ�
������������ߺ������Ƕ�Ӧ��ȣ������ASA��SAS֤����������ȫ�ȣ�
������������Ǻ���һ�߶�Ӧ��ȣ�����ASA֤����������ȫ��.
�����������������ĶԶ�ӦԪ����ȣ�������������һ��ȫ��.

 �ٷ�ѧ����ҵ��������ϵ�д�
�ٷ�ѧ����ҵ��������ϵ�д�