题目内容
【题目】有这样一个问题:探究函数y=x+|x﹣2|的图象与性质
小明根据学习函数的经验,对函数y=x+|x﹣2|的图象与性质进行了探究
下面是小明的探究过程,请补充完成:
(1)化简函数解析式,当x≥2时,y= ;当x<2时,y= ;
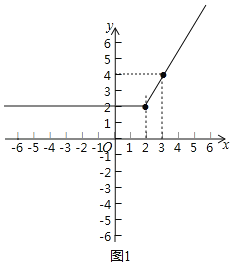
(2)根据(1)中的结果,请在图1的坐标系中画出函数y=x+|x﹣2|的图象;
(3)结合函数的图象,写出该函数的一条性质: ;
(4)结合画出的函数图象,利用图2解决问题,若关于x的方程ax+1=x+|x﹣2|有两个实数根,直接写出实数a的取值范围: .

【答案】(1)y=2x﹣2; y=2;(2)详见解析;(3)当x>2时,y随x的增大而增大;(4)0.5<a<2.
【解析】
(1)根据题目中的函数解析式,可以分别写出x≥2和x<2时的函数解析式;
(2)根据(1)中的结果,可以在图1的坐标系中画出函数y=x+|x﹣2|的图象;
(3)根据(1)中的函数图象,可以写出函数y=x+|x﹣2|的一条性质,本题答案不唯一,只要符合题意即可;
(4)根据一次函数与方程的关系,可以得到关于x的方程ax+1=x+|x﹣2|有两个实数根时,a的取值范围.
(1)当x≥2时,y=x+|x﹣2|=x+x﹣2=2x﹣2,
当x<2时,y=x+|x﹣2|=x+2﹣x=2,
故答案为:2x﹣2,2;
(2)当x≥2时,y=2x﹣2过点(2,2),(3,4),
函数y=x+|x﹣2|的图象如图1所示;
(3)由图象可知,
当x>2时,y随x的增大而增大,
故答案为:当x>2时,y随x的增大而增大;
(4)∵y=ax+1的函数图象一定过点(0,1)
∴当y=ax+1中的a=2时,直线y=ax+1与直线y=x+|x﹣2|有一个交点,
当a≥2或a<0时,y=ax+1与y=x+|x﹣2|有一个交点,
当直线y=ax+1过点(2,2)时,2=2a+1,得a=0.5,故当0≤a<0.5时,y=ax+1与y=x+|x﹣2|没有交点,当a=0.5时,y=ax+1与y=x+|x﹣2|有一个交点,
由上可得,关于x的方程ax+1=x+|x﹣2|有两个实数根,实数a的取值范围是:0.5<a<2,
故答案为:0.5<a<2.
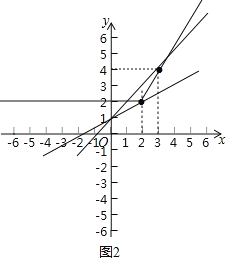

 阅读快车系列答案
阅读快车系列答案



