题目内容
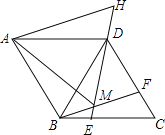
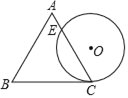
【题目】如图，△ABC中，AB＝AC＝10厘米，BC＝12厘米，D是BC的中点，点P从B出发，以a厘米/秒（a＞0）的速度沿BA匀速向点A运动，点Q同时以1厘米/秒的速度从D出发，沿DB匀速向点B运动，其中一个动点到达终点时，另一个动点也随之停止运动，设它们的运动时间为t秒.
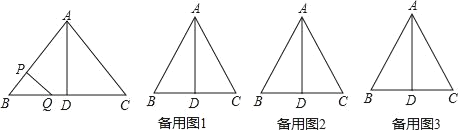
（1）若a＝2，那么t为何值时△BPQ与△BDA相似？
（2）已知M为AC上一点，若当t＝
时，四边形PQCM是平行四边形，求这时点P的运动速度.
（3）在P、Q两点运动过程中，要使线段PQ在某一时刻平分△ABD的面积，点P的运动速度应限制在什么范围内？（提示：对于一元二次方程，有如下的结论：若x1x2是方程ax2+bx+c＝0（a≠0）的两个根，则x1+x2＝﹣
，x1x2＝
）
【答案】(1)当a＝2时，t＝
秒或
秒时，△BPQ与△BDA相似;(2)点P的速度是2.5厘米/秒;(3)点P的速度应大于或等于
厘米/秒.
【解析】
（1）根据相似的性质，分情况讨论当△BPQ∽△BDA时及当△BQP∽△BDA时，进行列式计算即可得解；
（2）根据△BPQ∽△BAC，由相似比即可求出P的速度；
（3）根据△BEP∽△BDA，进而求出
和
的面积表达式后即可得解.
（1）当a＝2时，BP＝2t，DQ＝1×t＝t，
∵D是BC中点，BC＝12，
∴BD＝DC＝6，
∴
；
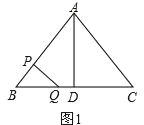
①当△BPQ∽△BDA时，如图1，
则有
，
∵BP＝2t，BD＝6，，BA＝10，
∴
，
解得：
；
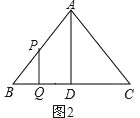
②当△BQP∽△BDA时，如图2，
则有
，
∵BP＝2t，BD＝6，，BA＝10，
∴
，
解得：
；
∴当a＝2时，秒或秒时，△BPQ与△BDA相似；
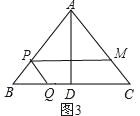
（2）当t＝
且四边形PQCM是平行四边形时，如图3，
则有PQ∥AC，BP＝a，DQ＝1×＝，BQ＝
，
∵PQ∥AC，
∴△BPQ∽△BAC，
∴
，
∵BP＝a，BA＝10，BQ＝
，BC＝12，
∴
，
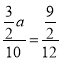解得：a＝2.5，
∴点P的速度是2.5厘米/秒；
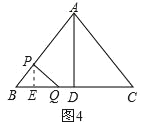
（3）作PE⊥BC，垂足为E，如图4，
∵AB＝AC，点D是BC的中点，
∴AD⊥BC，
∵AB＝10，BD＝6，
∴AD＝8，
∵PE⊥BC，AD⊥BC，
∴△BEP∽△BDA，
∴
，
∵AD＝8，BP＝at，BA＝10，
∴
，
∴
，
∴
，
∵线段PQ平分△ABD的面积，
∴
，
∴
，
整理得：
，
由题可得：
，
解得：
，
此时
，
∴方程
有两个小于6的正实根，
∴点P的速度应大于或等于厘米/秒.
