题目内容
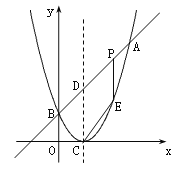
【题目】如图，已知抛物线与x轴交于A（﹣1，0）、E（3，0）两点，与y轴交于点B（0，3）．
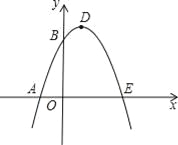
（1）求抛物线的解析式；
（2）设抛物线顶点为D，求四边形AEDB的面积；
（3）△AOB与△DBE是否相似？如果相似，请给以证明；如果不相似，请说明理由．
【答案】（1）
；（2）9；（3）△AOB∽△DBE.理由见解析.
【解析】
（1）易得c=3，故设抛物线解析式为y=ax2+bx+3，根据抛物线所过的三点的坐标，可得方程组，解可得a、b的值，即可得解析式；
（2）易由顶点坐标公式得顶点坐标，根据图形间的关系可得四边形ABDE的面积=
，代入数值可得答案；
（3）根据题意，易得∠AOB=∠DBE=90°，且
，即可判断出两三角形相似．
（1）∵抛物线与y轴交于点（0，3），
∴设抛物线解析式为y=ax2+bx+3（a≠0）
根据题意，得
，
解得
．
∴抛物线的解析式为y=﹣x2+2x+3；
（2）如图，设该抛物线对称轴是DF，连接DE、BD．过点B作BG⊥DF于点G．
由顶点坐标公式得顶点坐标为D（1，4）
设对称轴与x轴的交点为F
∴四边形ABDE的面积=
=
AOBO+（BO+DF）OF+EFDF
=×1×3+×（3+4）×1+×2×4
=9；
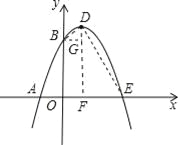
（3）相似，如图，
BD=
；
∴BE=
DE=
=
∴BD2+BE2=20，DE2=20
即：BD2+BE2=DE2，
所以△BDE是直角三角形
∴∠AOB=∠DBE=90°，且，
∴△AOB∽△DBE．
练习册系列答案
相关题目
