题目内容
【题目】如图1,抛物线y=﹣![]() 与x轴交于A、B两点,与y轴交于点C,连接AC、BC.
与x轴交于A、B两点,与y轴交于点C,连接AC、BC.
(1)求线段AC的长;
(2)如图2,E为抛物线的顶点,F为AC上方的抛物线上一动点,M、N为直线AC上的两动点(M在N的左侧),且MN=4,作FP⊥AC于点P,FQ∥y轴交AC于点Q.当△FPQ的面积最大时,连接EF、EN、FM,求四边形ENMF周长的最小值.
(3)如图3,将△BCO沿x轴负方向平移![]() 个单位后得△B'C'O',再将△B'C'O'绕点O'顺时针旋转α度,得到△B″C″O'(其中0°<α<180°),旋转过程中直线B″C″与直线AC交于点G,与x轴交于点H,当△AGH是等腰三角形时,求α的度数.
个单位后得△B'C'O',再将△B'C'O'绕点O'顺时针旋转α度,得到△B″C″O'(其中0°<α<180°),旋转过程中直线B″C″与直线AC交于点G,与x轴交于点H,当△AGH是等腰三角形时,求α的度数.
【答案】(1)6(2)![]() (3)α的值为15°或60°或105°或150°
(3)α的值为15°或60°或105°或150°
【解析】
(1)根据抛物线的解析式求出A,C两点坐标,可得OA=3![]() ,OC=3,利用勾股定理即可解决问题.
,OC=3,利用勾股定理即可解决问题.
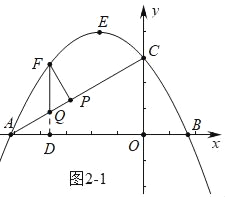
(2)如图2﹣1中,延长FQ交OA于D.设F(m,﹣![]() m2﹣
m2﹣![]() m+3),构建二次函数求出FQ的值最大时的点F的坐标,如图2﹣2中,作FF′∥AC,使得FF′=MN=4,作点F′关于直线AC的对称点F″,连接FF″交直线AC于点M,连接FM,EN,EF,此时四边形ENMF的周长最短.再求出点M.N的坐标即可解决问题.
m+3),构建二次函数求出FQ的值最大时的点F的坐标,如图2﹣2中,作FF′∥AC,使得FF′=MN=4,作点F′关于直线AC的对称点F″,连接FF″交直线AC于点M,连接FM,EN,EF,此时四边形ENMF的周长最短.再求出点M.N的坐标即可解决问题.
(3)分四种情形分别画出图象求解即可.
(1)由题意:A(﹣3![]() ,0),B(
,0),B(![]() ,0),C(0,3),
,0),C(0,3),
∴OA=3![]() ,OC=3,
,OC=3,
∴AC=![]() =6.
=6.
(2)如图2﹣1中,延长FQ交OA于D.设F(m,﹣![]() m2﹣
m2﹣![]() m+3),
m+3),
∵tan∠CAO=![]() =
=![]() ,
,
∴∠CAO=30°,∵FQ∥y轴,FP⊥AC,
∴∠ADQ=∠FPQ=90°,
∴∠AQD=∠FQP=60°,
∴当FQ最大时,△FPQ的面积最大,
∵直线AC的解析式为y=![]() x+3,
x+3,
∴Q(m,![]() m+3),
m+3),
∴FQ=﹣![]() m2﹣
m2﹣![]() m+3﹣
m+3﹣![]() m﹣3=﹣
m﹣3=﹣![]() m2﹣
m2﹣![]() m=﹣
m=﹣![]() (m+
(m+![]() )2+
)2+![]() ,
,
∵﹣![]() <0,
<0,
∴m=﹣![]() ,FQ的值最大,即△PFQ的面积最大,此时F(﹣
,FQ的值最大,即△PFQ的面积最大,此时F(﹣![]() ,
,![]() ),
),
如图2﹣2中,作FF′∥AC,使得FF′=MN=4,作点F′关于直线AC的对称点F″,连接FF″交直线AC于点M,连接FM,EN,EF,此时四边形ENMF的周长最短.
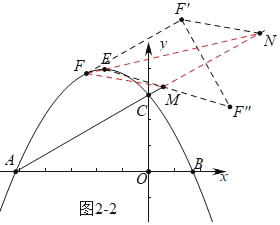
由题意点F向右平移2![]() 个单位,再向上平移2个单位得到点F′(
个单位,再向上平移2个单位得到点F′(![]() ,
,![]() ),
),
∵F″与F′关于直线AC对称,
∴F″(![]() ,
,![]() ),
),
∴M(![]() ),N(
),N(![]() ),
),
∵抛物线顶点E(﹣![]() ,4),
,4),
∴FM=![]() ,EN=
,EN=![]() =
=![]() ,EF=
,EF=![]() =
=![]() ,
,
∴四边形ENMF的周长的最小值为![]() .
.
(3)①如图3﹣1中,当AG=AH时
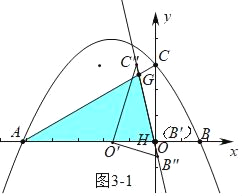
∵AG=AH,∠HAG=30°,
∴∠AHG=∠AGH=75°,
∵∠AHG=∠HO′B″+∠O′B″H,∠O′B″H=60°
∴∠HO′B″=15°,
∴α=15°
②如图3﹣2中,当HA=HG时,
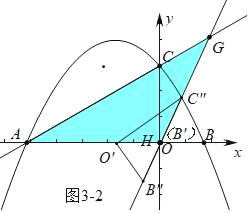
∵AG∥O′C″,
∴∠HO′C″=∠GAO=30°,
∴∠HO′B″=60°,
∴α=60°.
③如图3﹣3中,当AG=AH时,
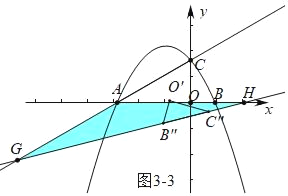
∵∠AGH=∠AHG=15°,
∵∠O′C″B″=∠C″O′H+∠AHG,
∴∠HO′C″=15°,
∴∠HO′B″=105°,
∴α=105°.
④如图3﹣4中,当GA=GH时,同法可得∠OO′B″=150°,α=150°.
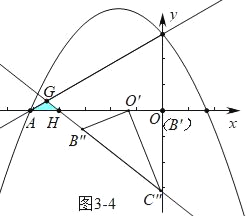
综上所述,满足条件的α的值为15°或60°或105°或150°.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某公司从2009年开始投入技术改造资金,经技术改进后,其产品的生产成本不断降低,具体数据如表:
年度 | 2009 | 2010 | 2011 | 2012 |
投入技改资金x(万元) | 2.5 | 3 | 4 | 4.5 |
产品成本y(万元/件) | 7.2 | 6 | 4.5 | 4 |
(1)试判断:从上表中的数据看出,y与x符合你学过的哪个函数模型?请说明理由,并写出它的解析式.
(2)按照上述函数模型,若2013年已投入技改资金5万元
①预计生产成本每件比2012年降低多少元?
②如果打算在2013年把每件产品的成本降低到3.2万元,则还需投入技改资金多少万元?