Question

【题目】已知一次函数y=kx+b的图象经过点(2,3),与y轴交于点B(0,4),与x轴交于点A.
（1）一次函数的表达式为;
（2）方程kx+b=0的解为;
（3）求该函数图象与两坐标轴围成的三角形的面积.

Answer 1

【答案】
（1）y=- x+4
（2）x=8
（3）S△AOB= ×4×8=16
【解析】解 ；（1）将点(2,3)与点B(0,4）分别代入y=kx+b得 ：

解得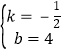
∴一次函数的表达式为 ；y=-x+4 ,
（2）把y=0代入y=-x+4 得；x=8 , 从而得出方程kx+b=0的解为x=8 ；
（3）∵A（8,0） ；B（0,4） ，
∴ OA=8 , OB=4 ,
∴S△AOB= OA·OB= ×4×8=16 .
（1）用待定系数法求出该函数的解析式；
（2）把把y=0代入y=-x+4 得；x=8 , 从而得出方程kx+b=0的解；
（3）根据A,B两点的坐标，求出OA,OB的长度，再根据三角形的面积计算公式计算出结果即可。
【考点精析】本题主要考查了确定一次函数的表达式的相关知识点，需要掌握确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法才能正确解答此题．