题目内容
如图,C是线段BD上一点,分别以BC、CD为边在BD同侧作等边△ABC和等边△CDE,AD交CE于F,BE交AC于G,则图中可通过旋转而相互得到的三角形对数有( ).

A.1对 B.2对 C.3对 D.4对

A.1对 B.2对 C.3对 D.4对
C
试题分析:根据等边三角形的三边相等、三个角都是60°,以及全等三角形的判定方法(SSS、SAS、ASA、AAS),全等三角形的性质,再结合旋转的性质即可得到结果.
△EBC≌△ACD,△GCE≌△FCD,△BCG≌△ACF.理由如下:
BC=AC,EC=CD,∠ACB=∠ECD,∠ACE是共同角?△EBC≌△ACD.
CD=EC,∠FCD=ECG,∠GEC=∠CDF?△GCE≌△FCD.
BC=AC,∠GBC=∠FAC,∠FCA=∠GCB?△BCG≌△ACF.
故选C.
点评:本题属于基础应用题,只需学生熟知等边三角形的性质、全等三角形的判定方法,即可完成.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
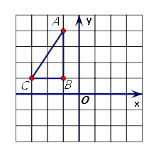

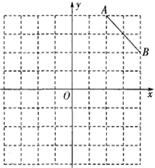

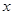 轴对称的图形△A1B1C1.
轴对称的图形△A1B1C1.


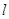 同侧有
同侧有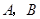 两个村庄,
两个村庄,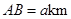
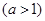 .现计划在河岸
.现计划在河岸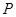 ,用输水管向两个村庄供水.
,用输水管向两个村庄供水.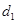 ,且
,且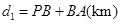 (其中
(其中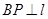 于点
于点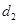 ,且
,且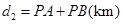 (其中点
(其中点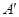 与点
与点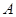 关于
关于 与
与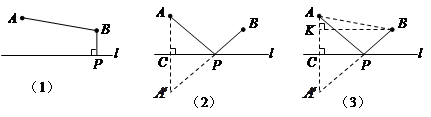
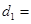 km(用含
km(用含 的式子表示);
的式子表示);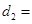 km(用含
km(用含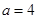 时,比较大小:
时,比较大小: (填“>”、“=”或“<”);
(填“>”、“=”或“<”);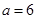 时,比较大小:
时,比较大小: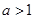 时)的所有取值情况进行分析,要使铺设的管道长度较短,应选择方案一还是方案二?
时)的所有取值情况进行分析,要使铺设的管道长度较短,应选择方案一还是方案二?