题目内容
在一平直河岸 同侧有
同侧有 两个村庄,
两个村庄,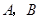 到
到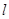 的距离分别是3km和2km,
的距离分别是3km和2km,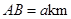
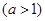 .现计划在河岸
.现计划在河岸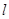 上建一抽水站
上建一抽水站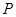 ,用输水管向两个村庄供水.
,用输水管向两个村庄供水.
方案设计
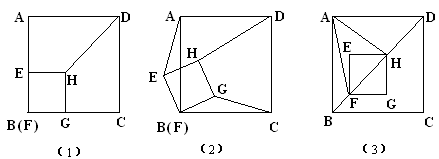
某班数学兴趣小组设计了两种铺设管道方案:图(1)是方案一的示意图,设该方案中管道长度为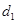 ,且
,且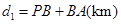 (其中
(其中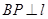 于点
于点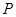 );图(2)是方案二的示意图,设该方案中管道长度为
);图(2)是方案二的示意图,设该方案中管道长度为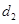 ,且
,且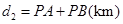 (其中点
(其中点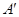 与点
与点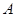 关于
关于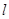 对称,
对称,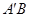 与
与 交于点
交于点 ).
).
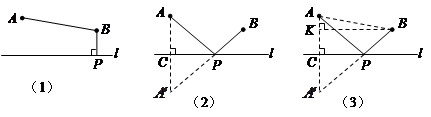
(1)观察计算
在方案一中,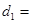 km(用含
km(用含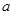 的式子表示);
的式子表示);
在方案二中,组长小宇为了计算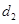 的长,作了如图(3)所示的辅助线,请你按小宇同学的思路计算,
的长,作了如图(3)所示的辅助线,请你按小宇同学的思路计算,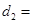 km(用含
km(用含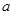 的式子表示).
的式子表示).
(2)探索归纳
①当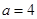 时,比较大小:
时,比较大小: (填“>”、“=”或“<”);
(填“>”、“=”或“<”);
当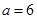 时,比较大小:
时,比较大小: (填“>”、“=”或“<”);
(填“>”、“=”或“<”);
②请你参考方框中的方法指导,就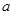 (当
(当 时)的所有取值情况进行分析,要使铺设的管道长度较短,应选择方案一还是方案二?
时)的所有取值情况进行分析,要使铺设的管道长度较短,应选择方案一还是方案二?
 同侧有
同侧有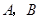 两个村庄,
两个村庄,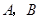 到
到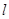 的距离分别是3km和2km,
的距离分别是3km和2km,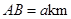
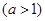 .现计划在河岸
.现计划在河岸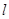 上建一抽水站
上建一抽水站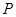 ,用输水管向两个村庄供水.
,用输水管向两个村庄供水.方案设计
某班数学兴趣小组设计了两种铺设管道方案:图(1)是方案一的示意图,设该方案中管道长度为
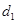 ,且
,且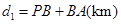 (其中
(其中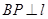 于点
于点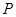 );图(2)是方案二的示意图,设该方案中管道长度为
);图(2)是方案二的示意图,设该方案中管道长度为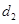 ,且
,且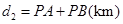 (其中点
(其中点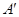 与点
与点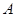 关于
关于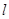 对称,
对称,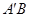 与
与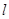 交于点
交于点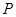 ).
).
(1)观察计算
在方案一中,
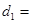 km(用含
km(用含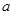 的式子表示);
的式子表示);在方案二中,组长小宇为了计算
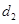 的长,作了如图(3)所示的辅助线,请你按小宇同学的思路计算,
的长,作了如图(3)所示的辅助线,请你按小宇同学的思路计算,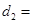 km(用含
km(用含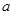 的式子表示).
的式子表示).(2)探索归纳
①当
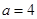 时,比较大小:
时,比较大小: (填“>”、“=”或“<”);
(填“>”、“=”或“<”);当
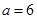 时,比较大小:
时,比较大小: (填“>”、“=”或“<”);
(填“>”、“=”或“<”);②请你参考方框中的方法指导,就
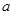 (当
(当 时)的所有取值情况进行分析,要使铺设的管道长度较短,应选择方案一还是方案二?
时)的所有取值情况进行分析,要使铺设的管道长度较短,应选择方案一还是方案二?
(1)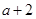 ; (2)
; (2)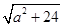 .
.
(2)①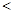 ;
; ;
;
②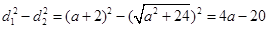 .
.
当 ,即
,即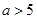 时,
时,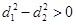 ,
,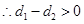 .
.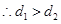 ;
;
当 ,即
,即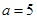 时,
时, ,
,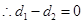 .
.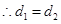 ;
;
当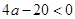 ,即
,即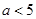 时,
时, ,
,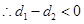 .
.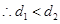 .
.
综上可知:当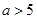 时,选方案二;当
时,选方案二;当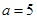 时,选方案一或方案二;当
时,选方案一或方案二;当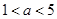 时,选方案一.
时,选方案一.
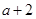 ; (2)
; (2)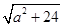 .
.(2)①
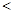 ;
;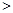 ;
; ②
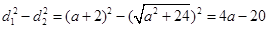 .
.当
 ,即
,即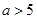 时,
时,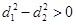 ,
,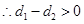 .
.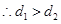 ;
;当
 ,即
,即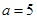 时,
时, ,
,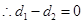 .
.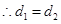 ;
;当
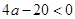 ,即
,即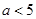 时,
时, ,
,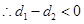 .
.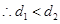 .
.综上可知:当
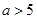 时,选方案二;当
时,选方案二;当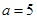 时,选方案一或方案二;当
时,选方案一或方案二;当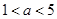 时,选方案一.
时,选方案一.观察计算:(1)由题意可以得知管道长度为d1=PB+BA(km),根据BP⊥l于点P得出PB=2,故可以得出d1的值为a+2.
(2)由条件根据勾股定理可以求出KB的值,由轴对称可以求出A′K的值,在Rt△KBA′由勾股定理可以求出A′B的值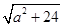 就是管道长度.
就是管道长度.
探索归纳:(1)①把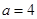 代入
代入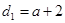 和
和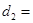
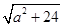 就可以比较其大小;
就可以比较其大小;
②把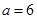 代入
代入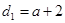 和
和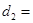
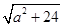 就可以比较其大小;
就可以比较其大小;
(2)分类进行讨论当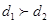 ,
,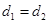 ,
,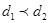 时就可以分别求出a的范围,从而确定选择方案.
时就可以分别求出a的范围,从而确定选择方案.
(2)由条件根据勾股定理可以求出KB的值,由轴对称可以求出A′K的值,在Rt△KBA′由勾股定理可以求出A′B的值
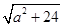 就是管道长度.
就是管道长度.探索归纳:(1)①把
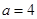 代入
代入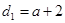 和
和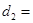
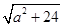 就可以比较其大小;
就可以比较其大小;②把
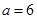 代入
代入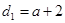 和
和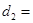
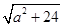 就可以比较其大小;
就可以比较其大小;(2)分类进行讨论当
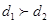 ,
,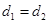 ,
,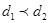 时就可以分别求出a的范围,从而确定选择方案.
时就可以分别求出a的范围,从而确定选择方案.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
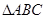 在正方形网格中,若点
在正方形网格中,若点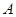 的坐标为
的坐标为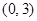 ,按要求回答下列问题:
,按要求回答下列问题: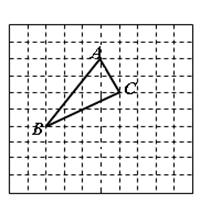
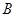 和点
和点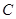 的坐标;
的坐标;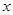 轴的对称图形
轴的对称图形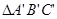 (不用写作法),并写出
(不用写作法),并写出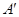 、
、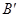 、
、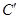 的坐标.
的坐标.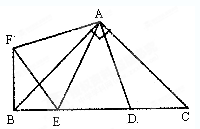
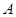 的坐标为
的坐标为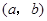 ,
,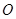 为坐标原点,连结
为坐标原点,连结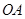 ,将线段
,将线段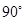 得
得 ,则点
,则点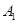 的坐标为( )
的坐标为( )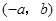
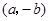
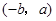
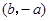

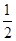 (∠1+∠2)
(∠1+∠2)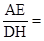 。
。 度(图2),⑴中的两个结论是否仍然成立?若成立,选择其中一个加以证明,若不成立,请说明理由。
度(图2),⑴中的两个结论是否仍然成立?若成立,选择其中一个加以证明,若不成立,请说明理由。