题目内容
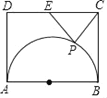
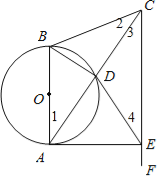
【题目】如图，在△ABC中，AB=CB，以AB为直径的⊙O交AC于点D．过点C作CF∥AB，在CF上取一点E，使DE=CD，连接AE．对于下列结论：①AD=DC；②△CBA∽△CDE；③
=
；④AE为⊙O的切线，一定正确的结论全部包含其中的选项是（ ）
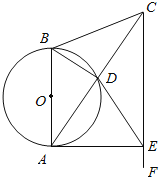
A. ①② B. ①②③ C. ①④ D. ①②④
【答案】D
【解析】
解：∵AB为直径，
∴∠ADB=90°，
∴BD⊥AC，
而AB=CB，
∴AD=DC，所以①正确；
∵AB=CB，
∴∠1=∠2，
而CD=ED，
∴∠3=∠4，
∵CF∥AB，
∴∠1=∠3，
∴∠1=∠2=∠3=∠4，
∴△CBA∽△CDE，所以②正确；
∵△ABC不能确定为直角三角形，
∴∠1不能确定等于45°，
∴和不能确定相等，所以③错误；
∵DA=DC=DE，
∴点E在以AC为直径的圆上，
∴∠AEC=90°，
∴CE⊥AE，
而CF∥AB，
∴AB⊥AE，
∴AE为⊙O的切线，所以④正确．
故答案为①②④．
练习册系列答案
阅读快车系列答案
相关题目
