题目内容
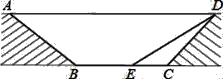
【题目】如图,![]() 和
和![]() 是两个全等的等腰直角三角形,
是两个全等的等腰直角三角形,![]() ,
,![]() 的顶点E与
的顶点E与![]() 的斜边BC的中点重合
的斜边BC的中点重合![]() 将
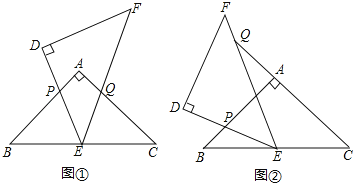
将![]() 绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q.
绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q.
![]() 如图
如图![]() ,当点Q在线段AC上,且
,当点Q在线段AC上,且![]() 时,
时,![]() 和
和![]() 的形状有什么关系,请证明;
的形状有什么关系,请证明;
![]() 如图
如图![]() ,当点Q在线段CA的延长线上时,
,当点Q在线段CA的延长线上时,![]() 和
和![]() 有什么关系,说明理由;
有什么关系,说明理由;
![]() 当
当![]() ,
,![]() 时,求P、Q两点间的距离.
时,求P、Q两点间的距离.
【答案】(1)见解析;(2)![]() ∽
∽![]() .理由见解析;(3)
.理由见解析;(3)![]() .
.
【解析】
(1)依据△ABC是等腰直角三角形,E是BC的中点,运用SAS即可判定△BPE≌△CQE;
(2)依据∠B=∠C=∠DEF=45°,即可得到∠BEP=∠EQC,再根据∠B=∠C,即可判定△BPE∽△CEQ;
(3)先根据△BPE∽△CEQ,得到![]() =
=![]() ,进而得到BE=CE=
,进而得到BE=CE=![]() ,BC=
,BC=![]() ,最后根据勾股定理,求得
,最后根据勾股定理,求得![]() △APQ中,PQ=
△APQ中,PQ=![]() .
.
![]() ≌
≌![]() .
.
理由![]() 是等腰直角三角形,
是等腰直角三角形,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 是BC的中点,
是BC的中点,
![]() ,
,
在![]() 和
和![]() 中,
中,
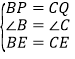 ,
,
![]() ≌
≌![]() ;
;
![]() ∽
∽![]() .
.
理由:![]() 和
和![]() 是两个全等的等腰直角三角形,
是两个全等的等腰直角三角形,
![]() ,
,
![]() ,
,
即![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ∽
∽![]() ;
;
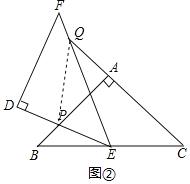
![]() 如图
如图![]() ,连结PQ,
,连结PQ,
![]() ∽
∽![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
在![]() 中,
中,![]() .
.

练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目