Question

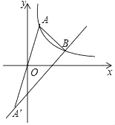
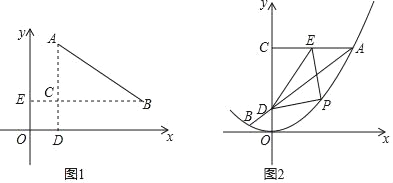
【题目】（1）如图1，若点A坐标为（x1，y1），点B坐标为（x2，y2），作AD⊥x轴于点D，BE⊥y轴于点E，AD与BE相交于点C，则有AC＝|y1﹣y2|，BC＝|x1﹣x2|，所以，A、B两点间的距离为AB＝．

根据结论，若M、N两点坐标分别为（1，4）、（5，1），则MN＝　 　（直接写出结果）．

（2）如图2，直线y＝kx+1与y轴相交于点D，与抛物线y＝x2相交于A，B两点，A点坐标为（4，a），过点A作y轴的垂线交y轴于点C，E是AC中点，点P是第一象限内直线AB下方抛物线上一动点，连接PE、PD、ED；

①a＝　 　，k＝　 　，AD＝　 　（直接写出结果）．

②若△DEP是以DE为底的等腰三角形，求点P的横坐标；

③求四边形CDPE的周长的最小值．

Answer 1

【答案】（1）5（2）①4，，5② ③5+

【解析】

（1）利用题目提供的两点间距离公式即可求解；

（2）①将点A的坐标代入二次函数表达式得：a＝×42＝4，则点A坐标为（4，4），将点A的坐标代入一次函数表达式得k＝，即可求解；

②利用PD＝PE，整理得：3x2+8x﹣38＝0，即可求解；

③在y轴上，截取CD′＝CD，连接D′E并延长交抛物线于点P，则此时，四边形CDPE的周长最小，最小值＝CD+CE+PD′＝5+PD′，即可求解．

（1）MN＝＝5，

故答案为5；

（2）①将点A的坐标代入二次函数表达式得：a＝×42＝4，则点A坐标为（4，4），点E的坐标为（2，4），

将点A的坐标代入一次函数表达式得：4＝4k+1，解得k＝，

∵CD＝3，CE＝4，

∴AD＝5，

故：答案为：4，，5；

②设点P的横坐标为x，即点P坐标为（x， x2），点D、E的坐标分别为（0，1）、（2，4），

由题意得：PD＝PE，即：PD2＝PE2，

x2+＝（x﹣2）2+（x2﹣4）2，整理得：3x2+8x﹣38＝0，

解得：x＝（负值已舍去），

即点P的横坐标为；

③在y轴上，截取CD′＝CD，连接D′E并延长交抛物线于点P，则此时，四边形CDPE的周长最小，

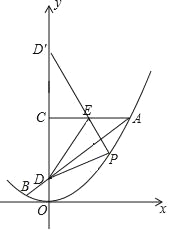
DE+PE＝PD′，点D′的坐标为（7，0），

四边形CDPE的周长最小值＝CD+CE+PD′＝5+PD′，

直线D′E的表达式为：y＝kx+7，把点E的坐标代入上式得：4＝2k+7，解得：k＝﹣，

则直线D′E的表达式为：y＝﹣x+7，

将该表达式与二次函数表达式联立并求解得：x＝﹣3，即点P的坐标为（﹣3，），

则PD′＝＝，

四边形CDPE的周长最小值＝5+．

故答案为：（1）5（2）①4，，5② ③5+ .