题目内容
【题目】我们发现:若AD是△ABC的中线,则有AB2+AC2=2(AD2+BD2),请利用结论解决问题:如图,在矩形ABCD中,已知AB=20,AD=12,E是DC中点,点P在以AB为直径的半圆上运动,则CP2+EP2的最小值是_____.
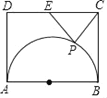
【答案】108
【解析】
设点O为AB的中点,连接EO交半圆于点P,此时PE取最小值,利用矩形的性质可求出EC、EP的值,则CP2+EP2=2PE2+CE2,代入数值即可求出结论.
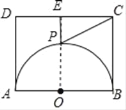
解:设点O为AB的中点,连接EO交半圆于点P,此时PE取最小值,
∵AB=20,四边形ABCD为矩形,
∴CD=AB,EO=AD,
∴OP=CE=![]() AB=10,
AB=10,
∴EP=OE﹣OP=AD﹣OP=2,
∴CP2+EP2=2PE2+CE2=2×22+102=108.
故答案为:108.

练习册系列答案
相关题目