题目内容
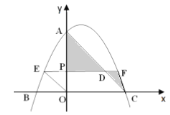
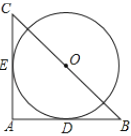
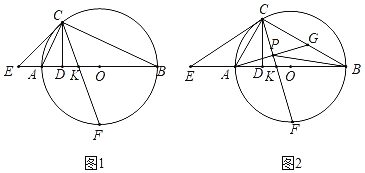
【题目】如图1,AB是⊙O的直径,C是⊙O上一点,CD⊥AB于D,E是BA廷长线上一点,连接CE,∠ACE=∠ACD,K是线段AO上一点,连接CK并延长交⊙O于点F.
(1)求证:CE是⊙O的切线;
(2)若AD=DK,求证:AKAO=KBAE;
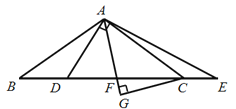
(3)如图2,若AE=AK,![]() ,点G是BC的中点,AG与CF交于点P,连接BP.请猜想PA,PB,PF的数量关系,并证明.
,点G是BC的中点,AG与CF交于点P,连接BP.请猜想PA,PB,PF的数量关系,并证明.
【答案】(1)详见解析;(2)详见解析;(3)PA2+PF2=PB2,证明详见解析.
【解析】
(1)连接OC,先由证明∠CAD=∠ACO,再由∠ACE=∠ACD,可证得∠ECO=90°,即可证明;
(2)先证得∠ACE=∠B,∠CAE=∠BKC,说明△CAE∽△BKC,利用相似三角形的性质推得ACKC=AEKB,再由∠CAD=∠CKD,∠CAD=∠OCA,判定△OCA∽△CAK,利用相似三角形的性质推得ACKC=AKAO,从而可得结论;
(3)结论:PA2+PF2=PB2.连接AF、BF,先证得∠ACE=∠CBE,∠E=∠E,从而△EAC∽△ECB,由相似三角形的性质推得BC=2AC,再设AC=CG=GB=x,则AG=![]() ,从而
,从而![]() ,结合∠PGB=∠BGA,可得△PGB∽△BGA,进而推得BP=BF=AF,然后运用勾股定理证即可得到结论.
,结合∠PGB=∠BGA,可得△PGB∽△BGA,进而推得BP=BF=AF,然后运用勾股定理证即可得到结论.
解:(1)证明:连接OC,如图所示:
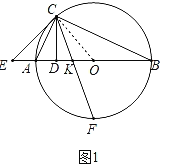
∵CD⊥AB,
∴∠CAD+∠ACD=90°,
∵OA=OC,
∴∠CAD=∠ACO,
又∵∠ACE=∠ACD,
∴∠ACE+∠ACO=90°,即∠ECO=90°,
∴CE是⊙O的切线;
(2)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠CAD+∠B=90°,
又∵∠CAD+∠ACD=90°,∠ACD=∠B,
∴∠ACE=∠B,
∵AD=DK,CD⊥AB,
∴CA=CK,∠CAD=∠CKD,
∴∠CAE=∠BKC,
∴△CAE∽△BKC,
∴![]() ,
,
∴ACKC=AEKB,
又∵∠CAD=∠CKD,∠CAD=∠OCA,
∴△OCA∽△CAK,
∴![]()
∴ACKC=AKAO,
∴AKAO=KBAE;
(3)PA2+PF2=PB2.理由如下:
如图,连接AF、BF,
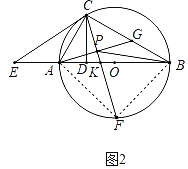
∵![]() ,
,
∴∠ACF=∠BCF=![]() ∠ACB=45°,AF=BF,
∠ACB=45°,AF=BF,
∴∠ECK=∠ACK+∠ACE=45°+∠ACE,∠EKC=∠BCK+∠KBC=45°+∠ABC,
∴∠ECK=∠EKC,
∴EC=EK=AE+EK=2AE,
∵∠ACE=∠CBE,∠E=∠E,
∴△EAC∽△ECB,
∴![]() ,
,
∴BC=2AC,
∵点G是BC的中点,
∴BC=2CG=2GB,
∴AC=CG,∠ACF=∠BCF,
∴CP⊥AG,AP=PG,
设AC=CG=GB=x,
则AG=![]() ,
,
∴![]() ,
,
又∠PGB=∠BGA,
∴△PGB∽△BGA,
∴∠GBP=∠GAB,
∴∠GBP+∠BCF=∠GAB+∠GAC,
即∠BPF=∠BAC=∠BFP,
∴BP=BF=AF,
∵在Rt△APF中,PA2+PF2=AF2,
∴PA2+PF2=PB2.

【题目】![]() ,
,![]() 两地相距
两地相距![]() ,甲、乙两人都由
,甲、乙两人都由![]() 地去
地去![]() 地,甲骑自行车,平均速度为
地,甲骑自行车,平均速度为![]() ;乙乘汽车,平均速度为
;乙乘汽车,平均速度为![]() ,且比甲晚
,且比甲晚![]() 出发.设甲的骑行时间为
出发.设甲的骑行时间为![]()
![]() .
.
(1)根据题意,填写表格:
时间 与 | 0.5 | 1.8 | |
甲与 | 5 | 20 | |
乙与 | 0 | 12 |
(2)设甲,乙两人与![]() 地的距离为
地的距离为![]() 和
和![]() .写出
.写出![]() ,
,![]() 关于
关于![]() 的表达式;
的表达式;
(3)设甲,乙两人之间的距离为![]() ,当
,当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
【题目】为弘扬祖国优秀传统文化,加强优秀文化熏陶,提高学生的文化素养和道德素质,我县某校举行了“经典启迪人生,国学伴我成长”主题活动,学校统一印制独具本校特色的国学教育校本教材,通过课堂教学和课外活动相结合的方式进行国学教育,为了解学生学习成果,现随机抽取了部分同学的国学成绩(x为整数,总分100分),绘制了如下尚不完整的统计图表.调查结果扇形统计图.
组别 | 成绩分组(单位:分) | 频数 | 频率 |
A | 50≤x<60 | 40 | 0.10 |
B | 60≤x<70 | 60 | c |
C | 70≤x<80 | a | 0.20 |
D | 80≤x<90 | 160 | 0.40 |
E | 90≤x<100 | 60 | 0.15 |
合计 | b | 1 |
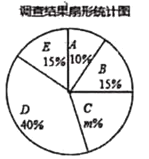
(1)根据以上信息解答问题:(1)统计表中a=________,b= ________,c=_______.
(2)扇形统计图中,m的值为________,“D”所对应的圆心角的度数是_______度;
(3)若参加国学教育的同学共有2000人,请你估计成绩在90分及以上的学生大约有多少人?