题目内容
【题目】如图所示,一条自西向东的观光大道l上有A、B两个景点,A、B相距2km,在A处测得另一景点C位于点A的北偏东60°方向,在B处测得景点C位于景点B的北偏东45°方向,求景点C到观光大道l的距离.(结果精确到0.1km)

【答案】解:如图,过点C作CD⊥l于点D,设CD=xkm,
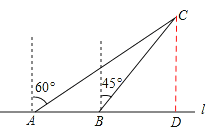
在△ACD中,∵∠ADC=90°,∠CAD=30°,
∴AD=![]() CD=
CD=![]() xkm。
xkm。
在△BCD中,∵∠BDC=90°,∠CBD=45°,
∴BD=CD=xkm。
∵AD﹣BD=AB,∴![]() x﹣x=2。∴x=
x﹣x=2。∴x=![]() +1≈2.7(km)。
+1≈2.7(km)。
答:景点C到观光大道l的距离约为2.7km.
【解析】
试题分析:过点C作CD⊥l于点D,设CD=xkm.先解直角△ACD,得出AD=![]() CD=
CD=![]() xkm,再解直角△BCD,得出BD=CD=xkm,然后根据AD﹣BD=AB,列出关于x的方程,解方程即可。
xkm,再解直角△BCD,得出BD=CD=xkm,然后根据AD﹣BD=AB,列出关于x的方程,解方程即可。

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目