题目内容
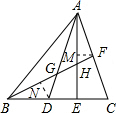
如图，△ABC中，E、D是BC边上的三等分点，F是AC的中点，BF交AD、AE于G、F，则BG：GH：HF等于（ ）
| A．1：2：3 | B．3：5：2 | C．5：3：2 | D．5：3：1 |
设BC=6a，则BD=DE=EC=2a，作FM∥BC交AE于点M，
∵F是AC的中点，
∴MF=
EC=a，
∵FM∥BC，
∴△BEH∽△FMH，
∴
=
=
=
，则HF=
BF，
作DN∥AC交BF于点N，设AC=2b，则AF=CF=b，
∴△BDN∽△BCF，
∴
=
=
=
=
，
∴DN=
CF=
b，BN=
BF，
∵DN∥AC，
∴△DNG∽△AFG，
∴
=
=
=
，
∴NG=
GF，即NG=
NF=
（BF-BN）=
（BF-
BF）=
BF，
∴BG=
GF+
GF=
BF，
∴GM=BF-BG-HF=BF-
BF-
BF=
BF，
∴BG：GH：HF=
BF：
BF：
BF=5：3：2．
故选C．
∵F是AC的中点，
∴MF=
| 1 |
| 2 |
∵FM∥BC，
∴△BEH∽△FMH，
∴
| HF |
| BH |
| MF |
| BE |
| a |
| 4a |
| 1 |
| 4 |
| 1 |
| 5 |
作DN∥AC交BF于点N，设AC=2b，则AF=CF=b，
∴△BDN∽△BCF，
∴
| BD |
| BC |
| ND |
| CF |
| BN |
| BF |
| 2a |
| 6a |
| 1 |
| 3 |
∴DN=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
∵DN∥AC，
∴△DNG∽△AFG，
∴
| NG |
| GF |
| DN |
| AF |
| ||
| b |
| 1 |
| 3 |
∴NG=
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 6 |
∴BG=
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 2 |
∴GM=BF-BG-HF=BF-
| 1 |
| 2 |
| 1 |
| 5 |
| 3 |
| 10 |
∴BG：GH：HF=
| 1 |
| 2 |
| 3 |
| 10 |
| 1 |
| 5 |
故选C．
练习册系列答案
阶梯计算系列答案
相关题目
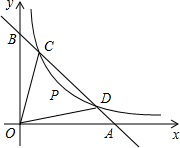，D（x2，y2），连接OC，OD（O是坐标原点），若∠BOC=∠AOD=α，且tanα=
