Question

【题目】点P是半径为4的⊙O外一点，PA是⊙O的切线，切点为A，且PA＝4，在⊙O内作长为4的弦AB，连接PB，则PB的长为_____．

Answer 1

【答案】4或4．

【解析】

分两种情况进行讨论：（1）弦AB在⊙O的同旁，可以根据已知条件证明△POA≌△POB，然后即可求出PA；

（2）弦AB在⊙O的两旁，此时可以根据已知条件证明PABO是平行四边形，然后利用平行四边形的性质和勾股定理即可求出PA．

解：连接OA，

（1）如图1，当弦AB与PA在O的同旁时，

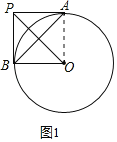
∵PA＝AO＝4，PA是⊙的切线，

∴∠AOP＝45°，

∵OA＝OB，

∴∠BOP＝∠AOP＝45°，

而OP＝OP，

∴△POA≌△POB（SAS），

∴PB＝PA＝4；

（2）如图2，当弦AB与PA在O的两旁，连接OA，OB，

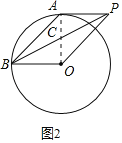
∵PA是⊙O的切线，

∴OA⊥PA，

而PA＝AO＝4，

∴OP＝4；

∵AB＝4，

而OA＝OB＝4，

∴AO⊥BO，

∴PABO是平行四边形，

∴PB，AO互相平分；

设AO交PB与点C，

即OC＝2，

∴BC＝，

∴PB＝4．

故答案为：4或4．