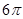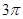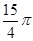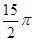题目内容
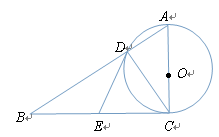
如图,在Rt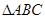 中,
中,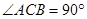 ,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于E.
,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于E.
(1)求证:点E是边BC的中点;
(2)求证: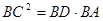 ;
;
(3)当以点O、D、E、C为顶点的四边形是正方形时,求证:△ABC是等腰直角三角形.
 中,
中,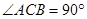 ,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于E.
,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于E.(1)求证:点E是边BC的中点;
(2)求证:
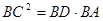 ;
;(3)当以点O、D、E、C为顶点的四边形是正方形时,求证:△ABC是等腰直角三角形.

.(1)证明见解析
(2)证明见解析
(3)证明见解析
(2)证明见解析
(3)证明见解析
试题分析:(1)由AC是直径,可得∠ADC=90°,从而可得∠BDC=90°,若要证明点E是BC边的中点,只需证明DE=CE=BE即可,由已知、切线的性质以及圆的性质就可以得到了;
由∠BDC=∠ACB,∠B=∠B可得△ABC∽△CDB,利用对应边成比例就可得到
当以点O、D、E、C为顶点的四边形是正方形时,可知∠OCD=45°,由AC是直径可得∠ADC=90°,从而得出∠A=45°继而得出△ABC是等腰直角三角形.
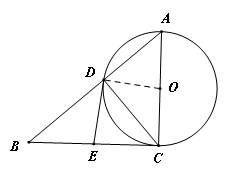
试题解析:(1)如图,连接OD.∵DE为切线,∴∠EDC+∠ODC=90°;
∵∠ACB=90°,∴∠ECD+∠OCD=90°.又∵OD=OC,∴∠ODC=∠OCD,
∴∠EDC=∠ECD,∴ED=EC;∵AC为直径,∴∠ADC=90°,
∴∠BDE+∠EDC=90°,∠B+∠ECD=90°,∴∠B=∠BDE,∴ED=DB.
∴EB=EC,即点E为边BC的中点;
(2)∵AC为直径,∴∠ADC=∠ACB=90°,又∵∠B=∠B
∴△ABC∽△CDB,∴
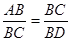 ,∴BC2=BD•BA;
,∴BC2=BD•BA;(3)当四边形ODEC为正方形时,∠OCD=45°;∵AC为直径,
∴∠ADC=90°,∴∠CAD=∠ADC﹣∠OCD=90°﹣45°=45°
∴Rt△ABC为等腰直角三角形.

练习册系列答案
相关题目

 ABCD的面积之比.
ABCD的面积之比.
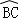 =
=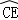 .
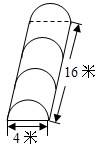
.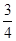 ,BC=3,求DE的长.
,BC=3,求DE的长.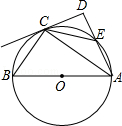
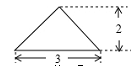
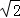 .若将BD绕点B旋转后,点D落在BC延长线上的点D′处,点D经过的路径为
.若将BD绕点B旋转后,点D落在BC延长线上的点D′处,点D经过的路径为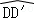 ,则图中阴影部分的面积是( )
,则图中阴影部分的面积是( )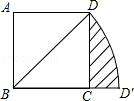
 ﹣1
﹣1
 ﹣
﹣