��Ŀ����
����Ŀ������֪������ֱ��y=x����ƽ��1����λ�ɵõ�һ�κ���y=x+1��ͼ��ֱ��y=kx(k��0)����ƽ��1����λ�ɵõ�һ�κ���y=k(x+1)��ͼ��������y=ax2(a��0)����ƽ��1����λ���ɵõ����κ���y=a(x+1)2��ͼ��.���Ƶģ����ǽ�����y=�Ox�O����ƽ��1����λ����ƽ��ֱ������ϵ�л������º����IJ���ͼ����ش��������⣺
(1)ƽ�ƺ�ĺ�������ʽ��__________��
(2)�������б���������Ϊ��ķ�������ƽ�ƺ�ĺ���ͼ��
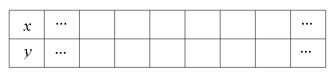
(3)��x ʱ��y��x�����������x ʱ��y��x���������С.
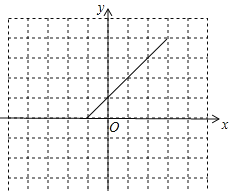
���𰸡�(1) ![]() ��(2) �������� (3)
��(2) �������� (3) ![]() ��
��![]() (���
(���![]() ����
����![]() ��>
��>![]() ����
����![]() ).
).
��������
(1)���ݲ��Ͽ��Եõ�ƽ�ƹ���:����Ҽ�;
(2)���ݺ���ͼ��ĶԳ��Ի���ͼ��;
(3)���ݺ���ͼ��ֱ�����.
(1) ![]() (д�ɷֶκ���Ҳ��)
(д�ɷֶκ���Ҳ��)
(2) ��ͼ��ʾ
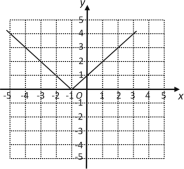
(3) ![]() ��
��![]() (���
(���![]() ����
����![]() ��
��![]() ����
����![]() )
)

��ϰ��ϵ�д�
�����Ŀ