题目内容
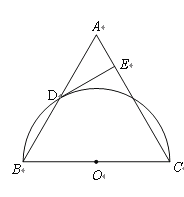
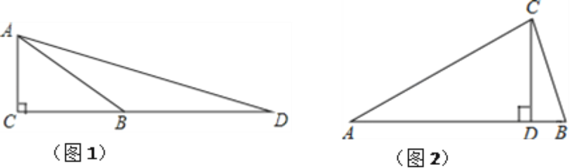
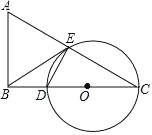
【题目】如图,在△ABC 中,∠ABC=90°,∠C=30°,AC 的垂直平分线交 BC 于点 D,交AC 于点 E.
(1)判断 BE 与△DCE 的外接圆⊙O 的位置关系,并说明理由;
(2)若 BE=![]() ,BD=1,求△DCE 的外接圆⊙O 的直径.
,BD=1,求△DCE 的外接圆⊙O 的直径.
【答案】(1)见解析;(2)△DCE的外接圆的直径是2.
【解析】
(1)连接OE,由DE是AC的垂直平分线,得到BE=CE,根据等腰三角形的性质得到∠EBC=∠C=30°,由三角形的内角和得到∠BEC=120°,由OE=OC,得到∠OEC=∠C=30°,求得∠BEO=90°,根据切线的判定定理即可得到结论;
(2)根据切割线定理得到BE2=BDBC,代入数据即可得到结论.
(1)连接OE,
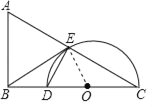
∵DE是AC的垂直平分线,
∴BE=CE,
∴∠EBC=∠C=30°,
∴∠BEC=120°,
∵OE=OC,
∴∠OEC=∠C=30°,
∴∠BEO=90°,
∴BE是⊙O的切线;
(2)∵BE是⊙O的切线,
∴BE2=BDBC,
即(![]() )2=1BC,
)2=1BC,
∴BC=3,
∴CD=2,
∴△DCE的外接圆的直径是2.

练习册系列答案
相关题目