Question

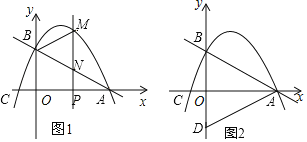
【题目】在平面直角坐标系内，反比例函数和二次函数y＝a（x2+x﹣1）的图象交于点A（1，a）和点B（﹣1，﹣a）．

（1）求直线AB与y轴的交点坐标；

（2）要使上述反比例函数和二次函数在某一区域都是y随着x的增大而增大，求a应满足的条件以及x的取值范围；

（3）设二次函数的图象的顶点为Q，当Q在以AB为直径的圆上时，求a的值．

Answer 1

【答案】（1）求直线AB与y轴的交点坐标（0，0）；（2）a＜0且x≤﹣；（3）a＝±．

【解析】

（1）由待定系数法可求直线AB解析式，即可求解；

（2）由反比例函数和二次函数都是y随着x的增大而增大，可得a＜0，又由二次函数y＝a（x2+x﹣1）的对称轴为x＝﹣，可得x≤﹣时，才能使得y随着x的增大而增大；

（3）先求点Q坐标，由OQ＝OA，可得方程，即可求a的值．

（1）设直线AB的解析式为：y＝kx+b，

由题意可得

∴b＝0，k＝a，

∴直线AB的解析式为：y＝ax，

∴当x＝0时，y＝0，

∴直线AB与y轴的交点坐标（0，0）；

（2）∵反比例函数过点A（1，a），

∴反比例函数解析式为：y＝，

∵要使反比例函数和二次函数都是y随着x的增大而增大，

∴a＜0．

∵二次函数y＝a（x2+x﹣1）＝a（x+）2﹣a，

∴对称轴为：直线x＝﹣．

要使二次函数y＝a（x2+x﹣1）满足上述条件，在k＜0的情况下，x必须在对称轴的左边，即x≤﹣时，才能使得y随着x的增大而增大．

综上所述，a＜0且x≤﹣；

（3）∵二次函数y＝a（x2+x﹣1）＝a（x+）2﹣a，

∴顶点Q（﹣，﹣a），

∵Q在以AB为直径的圆上，

∴OA＝OQ，

∴（﹣）2+（﹣）2＝12+a2，

∴a＝±