题目内容
【题目】已知抛物线
与
轴交于点
．
(1)求点的坐标和该抛物线的顶点坐标；
(2)若该抛物线与
轴交于
两点，求
的面积
；
(3)将该抛物线先向左平移
个单位长度，再向上平移
个单位长度，求平移后的抛物线的解析式（直接写出结果即可）．
【答案】（1）（0，5）；
；（2）15；（3）
【解析】
(1)令x=0即可得出点C的纵坐标，从而得出点C的坐标；利用配方法将抛物线表达式进行变形即可得出顶点坐标
(2)求出A，B两点的坐标，进而求出A与B的距离，由C点坐标可知OC的长，即可得出答案
(3)根据平移的规律结合原抛物线表达式 
即可得出答案.
解：（Ⅰ）当
时，
，故点
，
则抛物线的表达式为：，
故顶点坐标为：；
(2)令
，解得：
或
，
则
，
则
；
(3)∵
∴平移后的抛物线表达式为：
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
【题目】某校为了解七、八年级学生对“防溺水”安全知识的掌握情况，从七、八年级各随机抽取50名学生进行测试，并对成绩（百分制）进行整理、描述和分析．部分信息如下：
a．七年级成绩频数分布直方图：
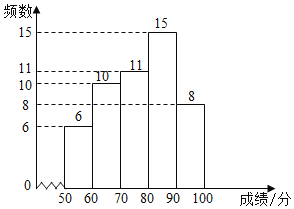
b．七年级成绩在
这一组的是：70 72 74 75 76 76 77 77 77 78 79
c．七、八年级成绩的平均数、中位数如下：
年级 | 平均数 | 中位数 |
七 | 76.9 | m |
八 | 79.2 | 79.5 |
根据以上信息，回答下列问题：
（1）在这次测试中，七年级在80分以上（含80分）的有 人；
（2）表中m的值为 ；
（3）在这次测试中，七年级学生甲与八年级学生乙的成绩都是78分，请判断两位学生在各自年级的排名谁更靠前，并说明理由；
（4）该校七年级学生有400人，假设全部参加此次测试，请估计七年级成绩超过平均数76.9分的人数．
