题目内容
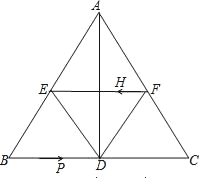
【题目】如图,在△ABC中,AB=AC,AD⊥BC于点D,BC=10cm,AD=8cm,E点F点分别为AB,AC的中点.
(1)求证:四边形AEDF是菱形;
(2)求菱形AEDF的面积;
(3)若H从F点出发,在线段FE上以每秒2cm的速度向E点运动,点P从B点出发,在线段BC上以每秒3cm的速度向C点运动,问当t为何值时,四边形BPHE是平行四边形?当t取何值时,四边形PCFH是平行四边形?
【答案】(1)证明见解析;(2)20;(3)2秒
【解析】试题分析:(1)根据等腰三角形的三线合一可得出D为BC的中点,结合E、F分别为AB、AC的中点可得出DE和DF是△ABC的中位线,根据中位线的定义可得出DE∥AC、DF∥AB,即四边形AEDF是平行四边形,根据三角形中位线定义可得出DE=![]() AC、DF=
AC、DF=![]() AB,结合AB=AC即可得出DE=DF,从而得出四边形AEDF是菱形;
AB,结合AB=AC即可得出DE=DF,从而得出四边形AEDF是菱形;
(2)根据中位线的定义可得出EF的长度,根据菱形的面积公式可求出菱形AEDF的面积;
(3)由中位线的定义可得出EF∥BC,根据平行四边形的判定定理可得出关于t的一元一次方程,解之即可得出结论.
详解:(1)证明:∵AB=AC,AD⊥BC,
∴D为BC的中点.
∵E、F分别为AB、AC的中点,
∴DE和DF是△ABC的中位线,
∴DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形.
∵E,F分别为AB,AC的中点,AB=AC,
∴AE=AF,
∴四边形AEDF是菱形,
(2)解:∵EF为△ABC的中位线,
∴EF=![]() BC=5.
BC=5.
∵AD=8,AD⊥EF,
∴S菱形AEDF=![]() ADEF=
ADEF=![]() ×8×5=20.
×8×5=20.
(3)解:∵EF∥BC,
∴EH∥BP.
若四边形BPHE为平行四边形,则须EH=BP,
∴5﹣2t=3t,
解得:t=1,
∴当t=1秒时,四边形BPHE为平行四边形.
∵EF∥BC,
∴FH∥PC.
若四边形PCFH为平行四边形,则须FH=PC,
∴2t=10﹣3t,
解得:t=2,
∴当t=2秒时,四边形PCFH为平行四边形.