题目内容
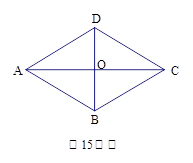
(11·贵港)如图所示,在矩形ABCD中,AB=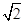 ,BC=2,对角线AC、BD
,BC=2,对角线AC、BD
相交于点O,过点O作OE垂直AC交AD于点E,则AE的长是
A.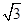 B.
B.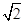 C.1 D.1.5
C.1 D.1.5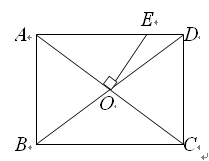
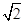 ,BC=2,对角线AC、BD
,BC=2,对角线AC、BD相交于点O,过点O作OE垂直AC交AD于点E,则AE的长是
A.
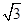 B.
B.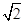 C.1 D.1.5
C.1 D.1.5
D
考点:
分析:先利用勾股定理求出AC的长,然后证明△AEO∽△ACD,根据相似三角形对应边成比例列式求解即可.
解答:解:∵AB=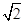
BC=2,∴AC=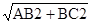 =
=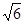
∴AO=
AC/2=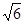 /2
/2
∵EO⊥AC,
∴∠AOE=∠ADC=90°,
又∵∠EAO=∠CAD,
∴△AEO∽△ACD,
∴AE/AC=AO/AD
,
即AE/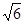 =
=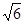 /2/2
/2/2
解得AE=1.5.
故选D.
点评:本题考查了矩形的性质,勾股定理,相似三角形对应边成比例的性质,根据相似三角形对应边成比例列出比例式是解题的关键.
分析:先利用勾股定理求出AC的长,然后证明△AEO∽△ACD,根据相似三角形对应边成比例列式求解即可.
解答:解:∵AB=
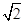
BC=2,∴AC=
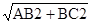 =
=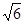
∴AO=
AC/2=
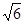 /2
/2∵EO⊥AC,
∴∠AOE=∠ADC=90°,
又∵∠EAO=∠CAD,
∴△AEO∽△ACD,
∴AE/AC=AO/AD
,
即AE/
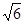 =
=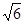 /2/2
/2/2解得AE=1.5.
故选D.
点评:本题考查了矩形的性质,勾股定理,相似三角形对应边成比例的性质,根据相似三角形对应边成比例列出比例式是解题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
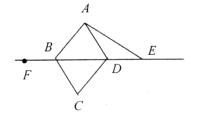
 中,
中, 为锐角,点
为锐角,点 为射线
为射线 上一点,联结
上一点,联结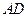 ,以
,以 .
. ,
, ,
,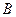 不重合),如图2,线段
不重合),如图2,线段 所在直线的位置关系为 __________ ,线段
所在直线的位置关系为 __________ ,线段


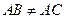 ,
, 是锐角,点
是锐角,点 满足什么条件时,
满足什么条件时, (点
(点 不重合),并说明理由.
不重合),并说明理由. 
 ?说明理由;
?说明理由;
 、
、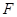 分别是平行四边形
分别是平行四边形 的边
的边 、
、 上的点,
上的点, 与
与 相交于点
相交于点 ,
, 与
与 相交于点
相交于点 ,若
,若 △APD
△APD 
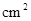 ,
,