题目内容
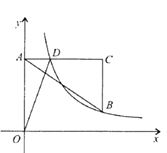
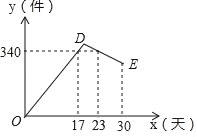
【题目】某公司开发出一款新的节能产品，该产品的成本价为6元件，该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试营销，售价为9元/件，工作人员对销售情况进行了跟踪记录，并将记录情况绘成图象，图中的折线ODE表示日销售量y(件)与销售时间x(天)之间的函数关系，已知线段DE表示的函数关系中，时间每增加1天，日销售量减少4件，
(1)请直接写出y与x之间的函数关系式；
(2)日销售利润不低于960元的天数共有多少天？试销售期间，日销售最大利润是多少元？
(3)工作人员在统计的过程中发现，有连续两天的销售利润之和为1980元，请你算出是哪两天．
【答案】（1）
；（2）试销售期间，日销售最大利润是1080元；（3）连续两天的销售利润之和为1980元的是第16，17两天和第25，26两天．
【解析】
（1）根据点D的坐标利用待定系数法即可求出线段OD的函数关系式，根据第23天销售了340件，结合时间每增加1天日销售量减少4件，即可求出线段DE的函数关系式，联立两函数关系式求出交点D的坐标，此题得解；
（2）分0≤x≤18和18＜x≤30，找出关于x的一元一次不等式，解之即可得出x的取值范围，有起始和结束时间即可求出日销售利润不低于960元的天数，再根据点D的坐标结合日销售利润=单件利润×日销售数，即可求出日销售最大利润;
(3) 设第x天和第（x＋1）天的销售利润之和为1980元,据此列出方程，根据取值范围解答即可.
（1）
（2）当0≤x≤18时，根据题意得，（9﹣6）×20x≥960，解得：x≥16；
当18＜x≤30时，根据题意得，（9﹣6）×（－4x＋432）≥960，解得：x≤28．
∴16≤x≤28． 28－16＋1＝13（天），
∴日销售利润不低于960元的天数共有13天．
由20x＝－4x＋432解得，x＝18，
当x＝18时，y＝20x＝360，∴点D的坐标为（18，360），
∴日最大销售量为360件，
360×（9－6）＝1080（元），
∴试销售期间，日销售最大利润是1080元．
（3）设第x天和第（x＋1）天的销售利润之和为1980元．
∵1980÷（9﹣6）＝660＜340×2，
∴x＜17，或x＋1＞23，
当x＜17时，根据题意可得20x＋20（x＋1）＝660，解得x＝16，符合，
当x＋1＞23时，－4x＋432－4（x＋1）＋432＝660，解得x＝25，符合，
∴连续两天的销售利润之和为1980元的是第16，17两天和第25，26两天．
