Question

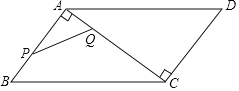
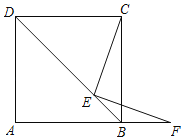
【题目】如图，在正方形ABCD中，E是对角线BD上一点，DE＝4BE，连接CE，过点E作EF⊥CE交AB的延长线于点F，若AF＝8，则正方形ABCD的边长为_____．

Answer 1

【答案】5

【解析】

由∠EHC＝∠BHF，∠CEH＝∠FBH＝90°可判定△ECH∽△BFH，从而得到∠ECH＝∠BFH；作辅助线可证明四边形ENBM是正方形，根据正方形的性质得EM＝EN，由角角边可证明△EMC≌△ENF，得CM＝FN；因DE＝4BE，△BEM∽△BDC，△BEN∽△BDA和线段的和差可求出正方形ABCD的边长．

解：如图所示：

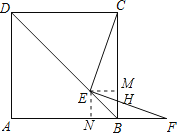
过点E作EM⊥BC，EN⊥AB，分别交BC、AB于M、N两点，

且EF与BC相交于点H．

∵EF⊥CE，∠ABC＝90°，∠ABC+∠HBF＝180°，

∴∠CEH＝∠FBH＝90°，

又∵∠EHC＝∠BHF，

∴△ECH∽△BFH（AA），

∴∠ECH＝∠BFH，

∵EM⊥BC，EN⊥AB，四边形ABCD是正方形，

∴四边形ENBM是正方形，

∴EM＝EN，∠EMC＝∠ENF＝90°，

在△EMC和△ENF中

,

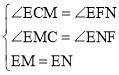∴△EMC≌△ENF（AAS）

∴CM＝FN，

∵EM∥DC，∴△BEM∽△BDC，

∴．

又∵DE＝4BE，

∴，

同理可得：，

设BN＝a，则AB＝5a，CM＝AN＝NF＝4a，

∵AF＝8，AF＝AN+FN，

∴8a＝8

解得：a＝1，

∴AB＝5

故答案为：5