题目内容
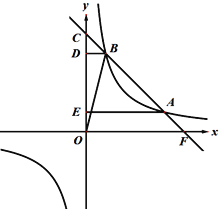
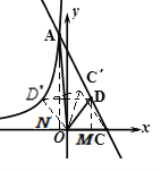
【题目】如图，在平面直角坐标系xOy中，函数y=2x+10的图像与函数y=
(x<0)的图像相交于点A，并与x轴交于点C.点D是线段上一点，△ODC与△OAC的面积比为1：3.若将△ODC绕点O逆时针旋转得到△OD′C′，当点D′第一次落在函数y=(x<0)的图像上时，C′的横坐标为_______.
【答案】
【解析】
过点A作
轴、
轴、连接D′D、C′C
∵函数
的图像与函数
的图像相交于点A
∴
解得：
，则
∴
点的坐标是
∵函数的图像与
轴交于C
当
时，
，解得
∴
点的坐标是
∴
∵△ODC与△OAC的面积比为1：3，且它们等高
∴△ODC与△OAC的对应边长比等于面积比，即
∵轴、轴
∴
∴
∴
，即
解得：
∴
点的横坐标为3，
代入函数中得：D点的纵坐标为4
∴点的坐标是
∴
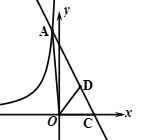
当点D′第一次落在函数的图像上时
设D′的坐标为
∴
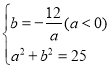变形得：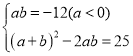
可得
解得：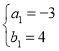
或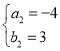
因为点D′是逆时针旋转第一次落在函数的图像上
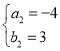∴不符合题意舍去，
故D′的坐标是
根据旋转的性质可得：
∵
∴在
中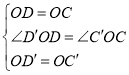
∴
∴
∵D′的坐标是，点的坐标是
∴
∴
设C′的坐标为
则
解得：
∴
∴C′的横坐标为
练习册系列答案
阅读快车系列答案
相关题目
