题目内容
【题目】点燃蜡烛,按照与时间成正比例关系变短,长21cm的蜡烛,已知点燃6分钟后,蜡烛变短3.6cm,设蜡烛点燃x分钟后变短ycm,求:
(1)用x表示函数y的解析式;
(2)自变量的取值范围;
(3)此蜡烛几分钟燃烧完?
(4)画出此函数的图像。
【答案】(1)y=0.6x;(2)0≤x≤35;(3)点燃35分钟后可燃烧光;(4)见解析.
【解析】
(1)根据燃烧的蜡烛=每分钟燃烧的长度×时间,建立函数关系式用待定系数法求解;
(2)当y=21时代入(1)的解析式就可以求出x的值从而可以求出结论;
(3)令y=21即可求得燃烧完使用的时间;
(4)根据自变量的取值范围知:此图象是一条线段,而不能画成直线或射线.
(1)设y=kx(k≠0),由题意,得
3.6=6k,
解得k=0.6,
则用x表示函数y的解析式为y=0.6x;
(2)当x=0时,y=0,
当y=21时,x=35
则自变量的取值范围是:0≤x≤35;
(3)当y=21时,0.6x=21,
∴x=35,
所以点燃35分钟后可燃烧光;
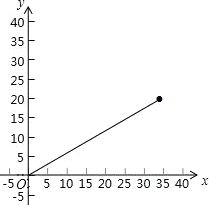
(4)如图,由x的取值范围:0≤x≤35;
列表为:
x | 0 | 35 |
y=0.6x | 0 | 21 |
图象是一条线段.描点并连线为:

练习册系列答案
相关题目