Question

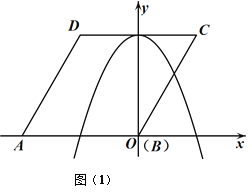
【题目】如图(1)，已知菱形的边长为，点在轴负半轴上，点在坐标原点，点的坐标为（，），抛物线顶点在边上，并经过边的中点．

（1）求这条抛物线的函数解析式；

（2）点关于直线的对称点是，求点到点的最短距离；

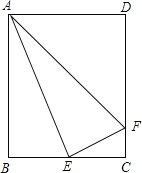
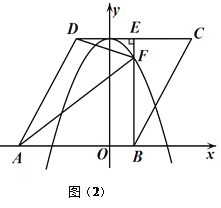
（3）如图（2）将菱形以每秒个单位长度的速度沿轴正方向匀速平移，过点作于点，交抛物线于点，连接、．设菱形平移的时间为秒（），问是否存在这样的，使与相似？若存在，求出的值；若不存在，请说明理由．

Answer 1

【答案】（1） （2）（3）存在t=1，使△ADF与△DEF相似

【解析】分析：(1)分别求出AB中点的坐标，抛物线的顶点坐标，再用待定系数法求抛物线的解析式；(2)；判断点C′在以M为圆心，长为半径的圆上；(3)∠DEF＝90°，∠DAF＜90°，所以分两种情况讨论，利用相似三角形的对应比成比例列方程求解.

详解：(1)由题意得AB的中点坐标为(，0)，抛物线的顶点坐标为(0，3)，分别代入y＝ax2＋b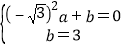，得，解得.

∴这条抛物线的函数解析式为.

(2)∵点C(，3)关于直线的对称点是C′，过点(0，3)，

∴C′一定在点(0，3)为圆心，为半径的圆上，

由勾股定理得AM＝，

当点A，C′，M在一条直线上时，AC′最小，最小值为AM－MC′，

即AC′的最小值为AM－MC′＝.

∴点C′到点A的最短距离为.

(3)如图2所示，在Rt△BCE中，∠BEC＝90°，BE＝3，BC＝，

∴，

∴∠C＝60°，∠CBE＝30°。∴EC＝BC＝，DE＝.

又∵AD∥BC，∴∠ADC＋∠C＝180°得∠ADC＝180°－60°＝120°，

要使△ADF与△DEF相似，则△ADF中必有一个角为直角，而∠DAF＜60°，

∴∠ADF＝90°或∠AFD＝90°.

(I)若∠ADF＝90°，∠EDF＝120°－90°＝30°，

在Rt△DEF中，DE＝，得EF＝1，DF＝2，

又∵E(t，3)，F(t，－t2＋3)，

∴EF＝3－(－t2＋3)＝t2，得∴t2＝1，∵t＞0，∴t＝1，

此时，∴.

又∵∠ADF＝∠DEF，∴△ADF∽△DEF，

(II)若∠DFA＝90°，可证得△DEF∽△FBA，则，

设EF＝m，则FB＝3－m，

∴，即m2－3m＋6＝0，此方程无实数根，

∴此时t不存在.

综上所述，存在t＝1，使△ADF与△DEF相似.