题目内容
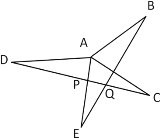
【题目】如图,已知AB⊥AC,AD⊥AE,AB=AC,AD=AE,
求证:(1)BE=DC
(2)BE⊥DC。
【答案】(1)见解析;(2)见解析.
【解析】
(1)由AB⊥AC,AD⊥AE,且AB=AC,AD=AE,利用SAS可判定△DAC≌△EAB,继而可证得BE=DC;
(2)由△DAC≌△EAB,可得∠ADC=∠AEB,然后根据∠ADC+∠APD=90°,通过等量代换可证得∠EQP=90°,问题得解.
证明:(1)∵AB⊥AC,AD⊥AE,
∴∠BAC=∠EAD=90°,
∴∠DAC=∠EAB,
在△DAC和△EAB中,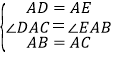 ,
,
∴△DAC≌△EAB(SAS),
∴BE=DC;
(2)∵△DAC≌△EAB,
∴∠ADC=∠AEB,
∵∠ADC+∠APD=90°,∠APD=∠EPQ,
∴∠AEB+∠EPQ=90°,
∴∠EQP=90°,
即BE⊥DC.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
【题目】某服装厂每天生产![]() 、
、![]() 两种品牌的服装共600件,
两种品牌的服装共600件,![]() 、
、![]() 两种品牌的服装每件的成本和利润如右表:
两种品牌的服装每件的成本和利润如右表:
A | B | |
成本(元/件) | 50 | 35 |
利润(元/件) | 20 | 15 |
设每天生产![]() 种品牌服装
种品牌服装![]() 件,每天两种服装获利
件,每天两种服装获利![]() 元.
元.
(1)请写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)如果服装厂每天至少投入成本26400元,那么每天至少获利多少元?
【题目】鞋号是指鞋子的大小,中国于60年代后期,在全国测量脚长的基础上制定了“中国鞋号”,1998年政府发布了基于![]() 系统,用毫米做单位的中华人民共和国国家标准
系统,用毫米做单位的中华人民共和国国家标准![]() ,被称为“新鞋号”,之前以厘米为单位的鞋号从此被称为“旧鞋号”.新旧鞋号部分对应表如下:
,被称为“新鞋号”,之前以厘米为单位的鞋号从此被称为“旧鞋号”.新旧鞋号部分对应表如下:
新鞋号 | 220 | 225 | 230 | 235 | … | 270 |
旧鞋号 | 34 | 35 | 36 | 37 | … |
|
(1)![]() 的值为______;
的值为______;
(2)若新鞋号为![]() ,旧鞋号为
,旧鞋号为![]() ,则把旧鞋号转换为新鞋号的公式为______
,则把旧鞋号转换为新鞋号的公式为______