题目内容
【题目】(1)某学校“智慧方园”数学社团遇到这样一个题目:
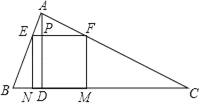
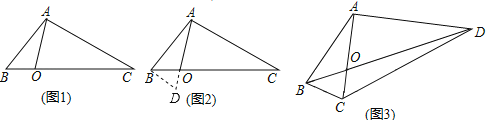
如图1,在![]() 中,点
中,点![]() 在线段
在线段![]() 上,
上,![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
经过社团成员讨论发现,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,通过构造
,通过构造![]() 就可以解决问题(如图
就可以解决问题(如图![]() .
.
请回答:![]()
![]() ,
,![]() .
.
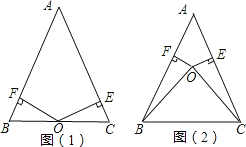
(2)请参考以上解决思路,解决问题:
如图3,在四边形![]() 中,对角线
中,对角线![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1) 75°;4![]() (2)
(2)![]()
【解析】
(1)根据平行线的性质可得出∠ADB=∠OAC=75°,结合∠BOD=∠COA可得出△BOD∽△COA,利用相似三角形的性质可求出OD的值,进而可得出AD的值,由三角形内角和定理可得出∠ABD=75°=∠ADB,由等角对等边可得出AB=AD=4![]() ,此题得解;
,此题得解;
(2)过点B作BE∥AD交AC于点E,同(1)可得出AE=4![]() ,在Rt△AEB中,利用勾股定理可求出BE的长度,再在Rt△CAD中,利用勾股定理可求出DC的长,此题得解.
,在Rt△AEB中,利用勾股定理可求出BE的长度,再在Rt△CAD中,利用勾股定理可求出DC的长,此题得解.
解:(1)∵BD∥AC,
∴∠ADB=∠OAC=75°.
∵∠BOD=∠COA,
∴△BOD∽△COA,
∴![]() .
.
又∵AO=3![]() ,
,
∴OD=![]() AO=
AO=![]() ,
,
∴AD=AO+OD=4![]() .
.
∵∠BAD=30°,∠ADB=75°,
∴∠ABD=180°-∠BAD-∠ADB=75°=∠ADB,
∴AB=AD=4![]()
故答案为:75;4![]() .
.
(2)过点B作BE∥AD交AC于点E,如图所示.
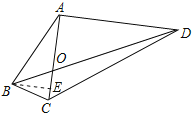
∵AC⊥AD,BE∥AD,
∴∠DAC=∠BEA=90°.
∵∠AOD=∠EOB,
∴△AOD∽△EOB,
∴![]() .
.
∵BO:OD=1:3,
∴![]()
∵AO=3![]() ,
,
∴EO=![]() ,
,
∴AE=4![]()
∵∠ABC=∠ACB=75°,
∴∠BAC=30°,AB=AC,
∴AB=2BE.
在Rt△AEB中,BE2+AE2=AB2,即(4![]() )2+BE2=(2BE)2,
)2+BE2=(2BE)2,
解得:BE=4,
∴AB=AC=8,AD=12.
在Rt△CAD中,AC2+AD2=CD2,即82+122=CD2,
解得:CD=4![]() .
.

 期末集结号系列答案
期末集结号系列答案【题目】某校有3000名学生.为了解全校学生的上学方式,该校数学兴趣小组以问卷调查的形式,随机调查了该校部分学生的主要上学方式(参与问卷调查的学生只能从以下六个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
种类 | A | B | C | D | E | F |
上学方式 | 电动车 | 私家车 | 公共交通 | 自行车 | 步行 | 其他 |
某校部分学生主要上学方式扇形统计图某校部分学生主要上学方式条形统计图
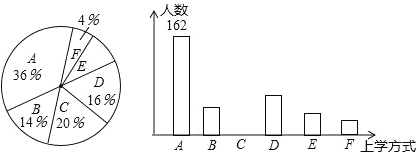
根据以上信息,回答下列问题:
(1)参与本次问卷调查的学生共有____人,其中选择B类的人数有____人.
(2)在扇形统计图中,求E类对应的扇形圆心角α的度数,并补全条形统计图.
(3)若将A、C、D、E这四类上学方式视为“绿色出行”,请估计该校每天“绿色出行”的学生人数.