Question

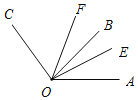
【题目】如图，OB为∠AOC内一条射线，∠AOB的余角是它自身的两倍．

（1）求∠AOB的度数；

（2）射线OE从OA开始，在∠AOB内以1°/s的速度绕着O点逆时针方向旋转，转到OB停止，同时射线OF在∠BOC内从OB开始以3°/s的速度绕O点逆时针方向旋转转到OC停止，设运动时间为t秒．

①若OE，OF运动的任一时刻，均有∠COF＝3∠BOE，求∠AOC的度数；

②OP为∠AOC内任一射线，在①的条件下，当t＝10时，以OP为边所有角的度数和的最小值为　 　．

Answer 1

【答案】（1）30°；（2）①120°，②170°.

【解析】

（1）根据余角的定义列方程解答即可；

（2）①分别用t的代数式表示出∠AOE、∠BOF，∠BOE，根据∠COF＝3∠BOE列方程解答即可；

②当OP与OB重合时，以OP为边所有角的度数和的有最小值，把t＝10代入计算即可．

解：（1）设∠AOB＝x，则∠AOB的余角＝（90﹣x），

依题意有：∴90﹣x＝2x，

∴x＝30，

∴∠AOB＝30°；

（2）①∵运动时间为t秒，则

∠AOE＝t°，∠BOF＝3t°，∠BOE＝（30﹣t）°，

∠COF＝∠AOC﹣∠AOB﹣∠BOF，

设∠AOC＝y°，

又∵∠COF＝3∠BOE，

则有：y﹣30﹣3t＝3（30﹣t），

解得：y＝120，

∴∠AOC＝120°，

②当OP与OB重合时，以OP为边所有角的度数和的有最小值，

当t＝10时，以OP为边所有角的度数和的最小值为170°．

故答案为：170°