Question

【题目】在Rt△ABC中，∠ACB=90°，AC=BC=1，将Rt△ABC绕A点逆时针旋转30°后得到Rt△ADE，点B经过的路径为 ， 则图中阴影部分的面积是 ．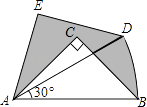

Answer 1

【答案】；
【解析】解：∵∠ACB=90°，AC=BC=1， ∴AB= = ，
∴点B经过的路径长= = ；
由图可知，S阴影=S△ADE+S扇形ABD﹣S△ABC ，
由旋转的性质得，S△ADE=S△ABC ，
∴S阴影=S扇形ABD= = ．
故答案为： ； ．
利用勾股定理列式求出AB，根据弧长公式列式计算即可求出点B经过的路径长，再根据S阴影=S△ADE+S扇形ABD﹣S△ABC ， 再根据旋转的性质可得S△ADE=S△ABC ， 然后利用扇形的面积公式计算即可得解．