Question

【题目】如图，线段AB经过圆心O，交⊙O于点A,C，点D在⊙O上，连接AD,BD，∠A=∠B=30°．

（1）求证：BD是⊙O的切线

（2）如果BD=2求OC的长

Answer 1

【答案】(1)证明见解析；(2) OC=.

【解析】试题分析：（1）连接OD，∠ADB是直角即可；

（2）在Rt△OBD中，利用有30°角的直角三角形所具有的特性即可解答.

试题解析：(1)连接OD，∵OA=OD，∴∠ADO=∠A=30°，∵∠A=∠B=30°，∴∠BDA=180°-（∠A+∠B）=120°，∴∠BDO=∠BDA-∠ADO=90°，即OD⊥BD.∴BD是⊙O 的切线．

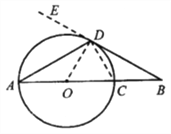
(2)∵∠B=30°，∠BDO=90°，BD=2 ， ∴OD=2×= ，∴OC=.