题目内容
【题目】如图,四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为16,则BE=( ) 
A.2
B.3
C.4
D.5
【答案】C
【解析】解:作BF⊥DC于F,如图, 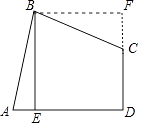
∵∠CDA=90°,BE⊥AD,BF⊥DF,
∴四边形BEDF为矩形,
∴∠EBF=90°,即∠EBC+∠CBF=90°,
∵∠ABC=90°,即∠EBC+∠ABE=90°,
∴∠ABE=∠CBE,
在△ABE和△CBF中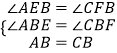 ,
,
∴△ABE≌△CBF,
∴BE=BF,S△ABE=S△CBF ,
∴四边形BEDF为正方形,四边形BEDF的面积=四边形ABCD的面积,
∴BE= ![]() =4.
=4.
故选C.
作BF⊥DC于F,如图,易得四边形BEDF为矩形,再证明△ABE≌△CBF得到BE=BF,S△ABE=S△CBF , 则可判断四边形BEDF为正方形,四边形BEDF的面积=四边形ABCD的面积,然后根据正方形的面积公式计算BE的长.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目



