题目内容
【题目】如图,已知直线a∥b,且a与b之间的距离为4,点A到直线a的距离为2,点B到直线b的距离为3,AB=2 ![]() .试在直线a上找一点M,在直线b上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,则此时AM+NB= .
.试在直线a上找一点M,在直线b上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,则此时AM+NB= . 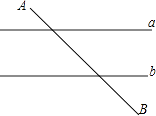
【答案】8
【解析】解:过A作直线a的垂线,并在此垂线上取点A′,使得AA′=4,连接A′B,与直线b交于点N,过M作直线a的垂线,交直线a于点N,连接AN,过点B作BE⊥AA′,交射线AA′于点E,如图.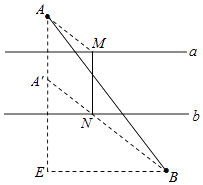
∵AA′⊥a,MN⊥a,
∴AA′∥MN.
又∵AA′=MN=4,
∴四边形AA′NM是平行四边形,
∴AM=A′N.
由于AM+MN+NB要最小,且MN固定为4,所以AM+NB最小.
由两点之间线段最短,可知AM+NB的最小值为A′B.
∵AE=2+3+4=9,AB=2 ![]() ,
,
∴BE= ![]() =
= ![]() ,
,
∵A′E=AE﹣AA′=9﹣4=5,
∴A′B= ![]() =8
=8
所以AM+NB的最小值为8.
所以答案是:8.
【考点精析】本题主要考查了轴对称-最短路线问题的相关知识点,需要掌握已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径才能正确解答此题.

练习册系列答案
相关题目