��Ŀ����
����Ŀ�����ı���ABCD��,AC��BD�ڵ�O,��AB��CD,������������˵��:
������ټ���������BC=AD��,��ô�ı���ABCDһ����ƽ���ı���;
������ټ�����������BAD=��BCD��,��ô�ı���ABCDһ����ƽ���ı���;
������ټ���������AO=OC��,��ô�ı���ABCDһ����ƽ���ı���;
������ټ�����������DBA=��CAB��,��ô�ı���ABCDһ����ƽ���ı���.
������ȷ��˵����( )
A.�٢�
B.�٢ۢ�
C.�ڢ�
D.�ڢۢ�
���𰸡�C
����������ͼ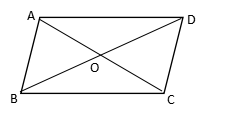
�ٵ�AB��CD��BC=AD�������ж��ı���ABCD��ƽ���ı��Σ���ˢٲ��������⣻
�ڡ�AB��CD
���ABD=��CDB
�ڡ�ABD�͡�CBD��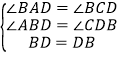
���ABD�ա�CBD
��AB=CD AB��CD
���ı���ABCD��ƽ���ı��Σ���ˢڷ������⣻
�ۡ�AB��CD
���ABD=��CDB
�ڡ�ABO�͡�CDO��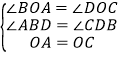
���ABO�ա�CDO
��AB=CD AB��CD
���ı���ABCD��ƽ���ı��Σ���ˢ۷������⣻
������ټ�����������DBA=��CAB��,�����ж��ı���ABCD��ƽ���ı��Σ���ˢܲ��������⣻
������ȷ��˵���Тڢ�
�ʴ�Ϊ��C
ƽ���ı��ε������ж������ֱ��ǣ���1������Ա߷ֱ�ƽ�е��ı�����ƽ���ı��Σ���2������Ա߷ֱ���ȵ��ı�����ƽ���ı��Σ���3��һ��Ա�ƽ������ȵ��ı�����ƽ���ı��Σ���4������ԽǷֱ���ȵ��ı�����ƽ���ı��Σ���5���Խ�����ƽ�ֵ��ı�����ƽ���ı��Σ�����ƽ���ı��ε��ж���������ѡ���е���������һ������֤��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ����һ��һ�ȵĹ���ѧ�����ʲ����У�������ѧ��ȫУ2000��������1000m���Գɼ������˳�飬ѧУ�ӳ����꼶��ȡ��һ���������ijɼ��������Ƴ�ͳ�Ʊ������Ƴ�Ƶ��ֱ��ͼ��
��� | ��Χ����λ���룩 | Ƶ�� | Ƶ�� |
1 | 170��x��200 | 5 | 0.1 |
2 | 200��x��230 | 13 | a |
3 | 230��x��260 | 15 | 0.3 |
4 | 260��x��290 | c | d |
5 | 290��x��320 | 5 | 0.1 |
6 | 320��x��350 | 2 | 0.04 |
7 | 350��x��380 | 2 | 0.04 |
�ϼ� | b | 1.00 |
��1������������У�������ʲô��
��2��ֱ��д��a��b��c��d��ֵ��
��3����ȫƵ��ֱ��ͼ��
��4�����б�ҵ�����ܲ�����Ŀ�ɼ�������������1000m������4��20�壨��260�룩Ϊ�ϸ����ܹ��Ƴ���У����������1000m�ĺϸ�����������ܣ�������ϸ��������������ܣ���˵�����ɣ�