题目内容
【题目】已知直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,抛物线
两点,抛物线![]() 经过
经过![]() 、
、![]() 两点,与
两点,与![]() 轴的另一个交点为
轴的另一个交点为![]() ,且
,且![]() .
.
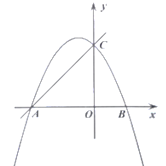
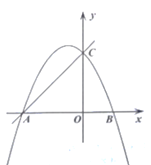
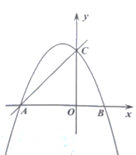
(1)求抛物线的解析式;
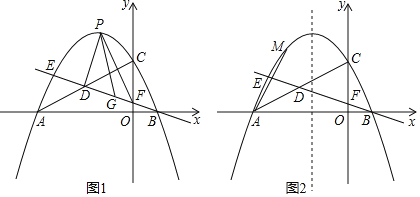
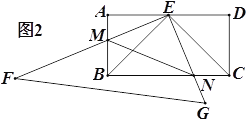
(2)点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,点
,点![]() 为第一象限内的一点,当
为第一象限内的一点,当![]() 是以
是以![]() 为斜边的等腰直角三角形时,连接
为斜边的等腰直角三角形时,连接![]() ,设
,设![]() 的长度为
的长度为![]() ,
,![]() 的面积为
的面积为![]() ,请用含
,请用含![]() 的式子表示
的式子表示![]() ,并写出自变量
,并写出自变量![]() 的取值范围;
的取值范围;
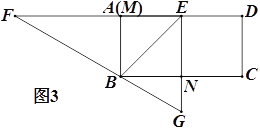
(3)在(2)的条件下,连接![]() 、
、![]() ,将
,将![]() 沿
沿![]() 翻折到
翻折到![]() 的位置(
的位置(![]() 与
与![]() 对应),若
对应),若![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() (0<t<4);(3)K(1,-1)
(0<t<4);(3)K(1,-1)
【解析】
(1)利用![]() 求出点C、A的坐标及点B的坐标,即可代入
求出点C、A的坐标及点B的坐标,即可代入![]() 求出解析式;
求出解析式;
(2)过点D作DE⊥x轴于E,作QF⊥DE于F,设QF=m,根据△QDF≌△DPE 求出FD=4+t-m,EP=4-t+m,解出m=t ,即可根据三角形的面积公式计算得到函数解析式及t的取值范围;
(3)作PL∥OQ ,GM⊥AB于M ,KN⊥AB于N,证得 △PGL≌△QGC,得到GP=GQ,根据勾股定理求出t,再证明四边形PGDK为正方形,根据正方形的性质及△GMP≌△PNK求出AN及ON即可.
(1)解:当x=0时,y=4,∴C(0,4)
当y=0时,x=-4,∴A(-4,0)
∵OC=2OB,
∴OB=2 ,
∴B(2,0)
代入抛物线解析式得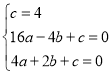 ,
,
解得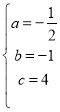 ,
,
∴抛物线的解析式为![]() ;
;
(2)过点D作DE⊥x轴于E,作QF⊥DE于F,
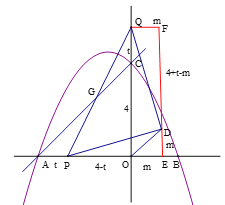
∴四边形QOEF为矩形
∴QF=OE,QO=FE,
设QF=m,
∵△QDF≌△DPE ,
∴QF=DE=m ,FD=EP,
∵FD=4+t-m,EP=4-t+m,
∴4-t+m=4+t-m,
∴m=t ,
∵OP=4-t,
∴![]() (0<t<4),
(0<t<4),
(3)作PL∥OQ ,GM⊥AB于M ,KN⊥AB于N,
∵OC=OA,
∴PL=PA ,
∵PA=CQ,
∴PL=CQ,
∴△PGL≌△QGC,
∴GP=GQ,
∵OG=![]() ,
,
∴PQ=![]() ,
,
在Rt△OPQ中,得(4-t)2+(4+t)2=![]() ,
,
∴t=2 ,
∵△PDG为等腰直角三角形,
∴四边形PGDK为正方形,
∵OQ=6,
∴GM=3,
∵GP=GO,
∴PM=MO=1,
∵△GMP≌△PNK,
∴GM=PN=3,PM=KN=1,
∴AN=5,ON=1,
∴K(1,-1)


 阅读快车系列答案
阅读快车系列答案